التحليل الأولي |التحليل الكامل |طريقة التحليل الشجري
مدونة ضوء التعليمية تقدم لكم درس “التحليل الأولي |التحليل الكامل |طريقة التحليل الشجري
” نترككم مع المقال:
اشترك في موقعنا ◀️ قناة يوتيوب 🔴 للحصول على أحدث مقاطع الفيديو والتحديثات والنصائح.
التحليل الأولي أو التحليل الكامل للرقم المحدد هو التعبير عن رقم معين كحاصل ضرب العامل الأولي.
عندما يتم التعبير عن عدد كحاصل ضرب عوامله الأولية، يطلق عليه اسم التحليل الأولي.
على سبيل المثال، 15 = 3 × 5. إذن، 3 و5 عوامل أولية للعدد 15.
العوامل الأولية لعدد ما هي دائمًا أعداد أولية، وعندما يتم التعبير عن الرقم كحاصل ضرب أعداد أولية، يطلق عليه اسم التحليل الأولي. يمكن إجراء التحليل الأولي باستخدام طريقتين: طريقة القسمة وطريقة شجرة العوامل.
يمكن الحصول على HCF المكون من رقمين أو أكثر عن طريق التحليل الأولي. لإيجاد HCF عن طريق التحليل الأولي، نقوم أولاً بإيجاد جميع العوامل الأولية للأعداد المحددة ثم إيجاد حاصل ضرب جميع العوامل الأولية المشتركة. المنتج هو HCF للأرقام المحددة.
طريقة شجرة العوامل:
نكتب أزواجًا من العوامل للعدد المعطى في دوائر تشكل فروعًا لشجرة العوامل.
طريقة التقسيم:
قسمة الأعداد المعطاة على أصغر عدد أولي. استمر في التقسيم حتى لا يكون قابلاً للقسمة مرة أخرى. يتوقف التحليل عندما نصل إلى عدد أولي.
لاحظ الأمثلة التالية للتحليل الأولي في طريقتين، أي طريقة شجرة العوامل وطريقة القسمة.
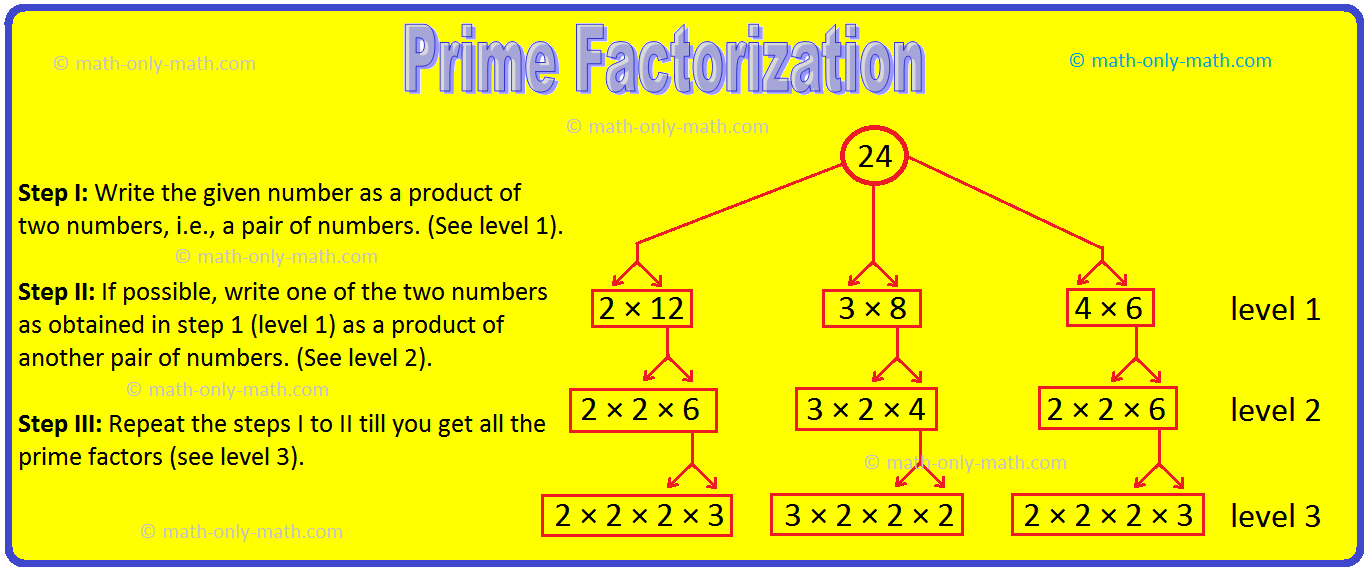
1. دعونا نتحقق من هذه العملية عن طريق عمل شجرة عوامل للرقم 24.
قواعد العمل للعثور على التحليل الأولي باستخدام طريقة شجرة العوامل:
الخطوة الأولى: اكتب الرقم المعطى كحاصل رقمين، أي زوج من الأرقام. (انظر المستوى 1).
الخطوة الثانية: إذا أمكن، اكتب أحد الرقمين اللذين تم الحصول عليهما في الخطوة 1 (المستوى 1) كحاصل ضرب زوج آخر من الأرقام. (انظر المستوى 2).
الخطوة الثالثة: كرر الخطوات من الأول إلى الثاني حتى تحصل على جميع العوامل الأولية (انظر المستوى 3).
نحصل على نفس العوامل في كل مربع في المستوى الأخير، أي المستوى 3
وبالتالي فإن العوامل 2 و 3 هي أعداد أولية.
رئيس الوزراء التخصيم ملكية: كل رقم أكبر من 1 له عامل أولي واحد بالضبط.
قواعد عمل التخصيم الأولي:
الخطوة الأولى: اقسم الرقم على أصغر عدد أولي (أصغر).
الخطوة الثانية: استمر في العملية حتى يتم الحصول على رقم أولي كالباقي.
2. أوجد التحليل الأولي للعدد 36.
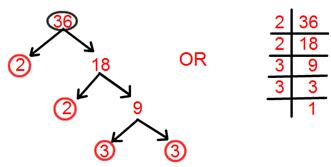
التحليل الأولي لـ 36 = 2 × 2 × 3 × 3.
= 2² × 3².
[Here two ways to solve factorisation one is tree factorisation method and the other one is by dividing.]
3. أوجد التحليل الأولي للعدد 32.
حل:
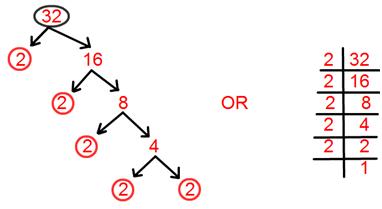
التحليل الأولي لـ 32 = 2 × 2 × 2 × 2 × 2.
= 2⁵.
4. أوجد التحليل الأولي للعدد 51.
حل:

التحليل الأولي لـ 51 = 3 × 17.
= 3¹ × 17¹
= 3 × 17.
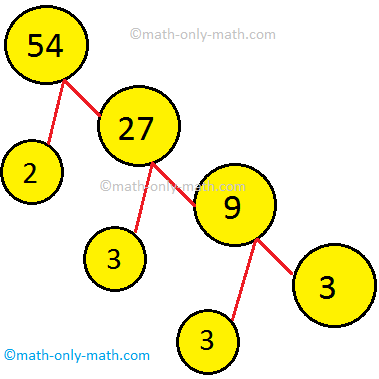
5. ارسم شجرة عوامل لإظهار التحليل الأولي للعدد 54.
حل:
6. أوجد التحليل الأولي للعدد 57.
حل:

التحليل الأولي لـ 57 = 3 × 19
= 3¹ × 19¹
= 3 × 19.
7. أوجد التحليل الأولي للعدد 60.
حل:
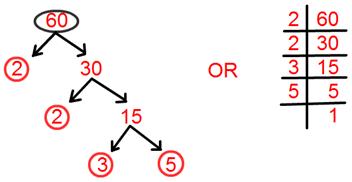
التحليل الأولي لـ 60 = 2 × 2 × 3 × 5.
= 2² × 3 × 5.
8. أوجد التحليل الأولي للعدد 63.
حل:
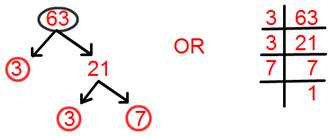
التحليل الأولي لـ 63 = 3 × 3 × 7.
= 3² × 7.
9. أوجد التحليل الأولي للعدد 72.
حل:
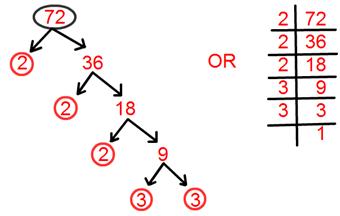
التحليل الأولي لـ 72 = 2 × 2 × 2 × 3 × 3.
= 2³ × 3².
10. أوجد التحليل الأولي للعدد 75.
حل:
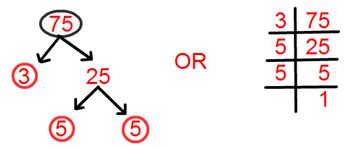
التحليل الأولي لـ 75 = 3 × 5 × 5.
= 3 × 5².
11. أوجد التحليل الأولي للعدد 78.
حل:
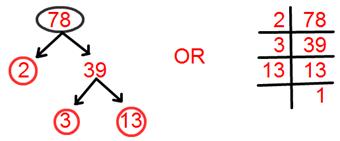
التحليل الأولي لـ 78 = 2 × 3 × 13.
12. أوجد التحليل الأولي للعدد 93.
حل:

التحليل الأولي لـ 93 = 3 × 31.
13. أوجد التحليل الأولي للعدد 102.
حل:

التحليل الأولي لـ 102 = 2 × 3 × 17.
14. أوجد التحليل الأولي للعدد 120.
حل:
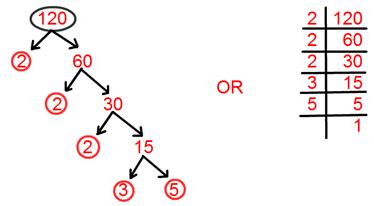
التحليل الأولي لـ 120 = 2 × 2 × 2 × 3 × 5.
= 2³ × 3 × 5.
15. أوجد التحليل الأولي للعدد 225.
حل:
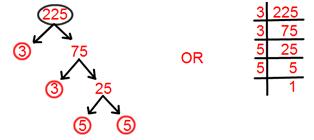
التحليل الأولي لـ 225 = 3 × 3 × 5 × 5.
= 3² × 5².
16. أوجد التحليل الأولي للعدد 243.
حل:
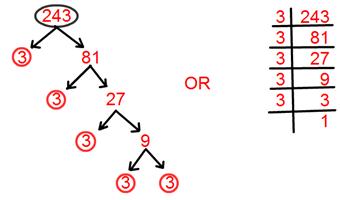
التحليل الأولي لـ 243 = 3 × 3 × 3 × 3 × 3.
= 3⁵.
17. أوجد التحليل الأولي للعدد 360.
حل:
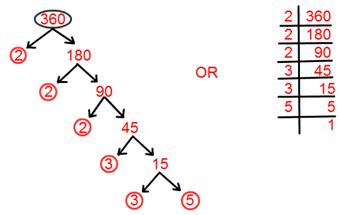
التحليل الأولي لـ 360 = 2 × 2 × 2 × 3 × 3 × 5.
= 2³ × 3² × 5.
18. اكتب العوامل الأولية للعدد 150 بطريقة شجرة العوامل وطريقة القسمة.
حل:
طريقة شجرة العوامل:
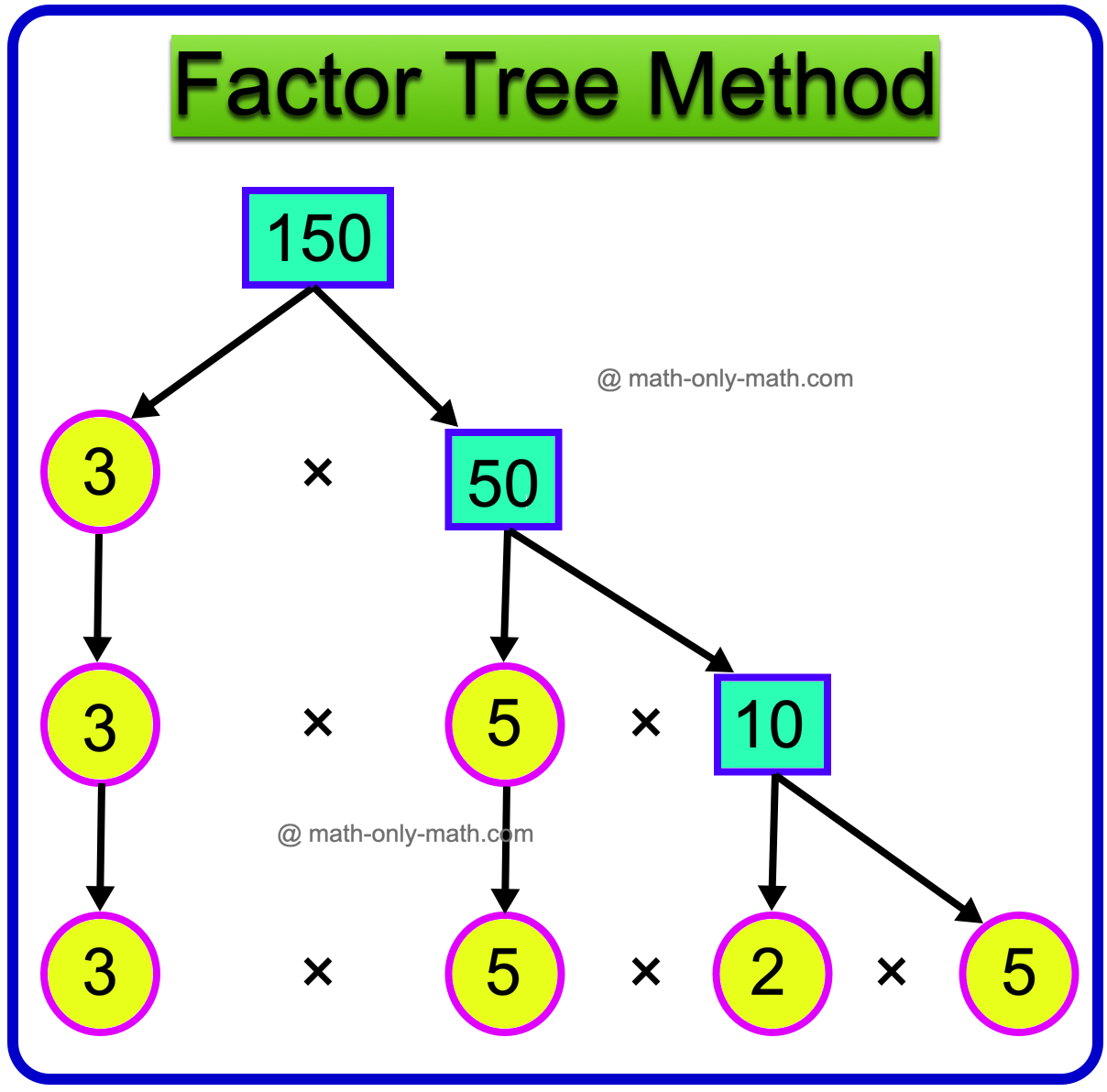
وبالتالي 150 = 3 × 5 × 2 × 5
ومن ثم، فإن العوامل الأولية للعدد 150 هي 2, 3, 5.
طريقة التقسيم:
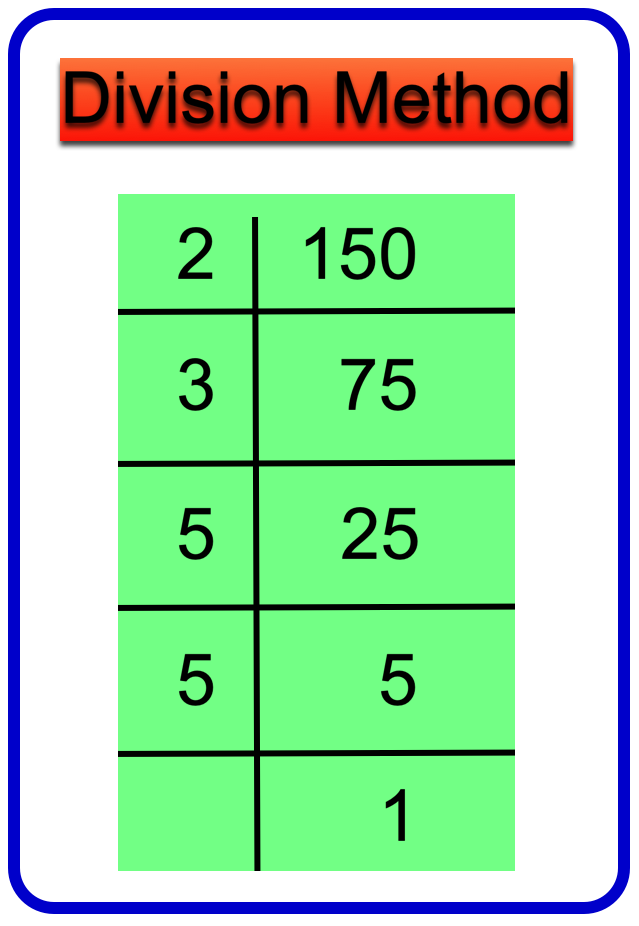
وبالتالي 150 = 2 × 3 × 5 × 5
ومن ثم، فإن العوامل الأولية للعدد 150 هي 2, 3, 5.
18. أوجد التحليل الأولي للرقم 1440 باستخدام طريقة القسمة.
حل:
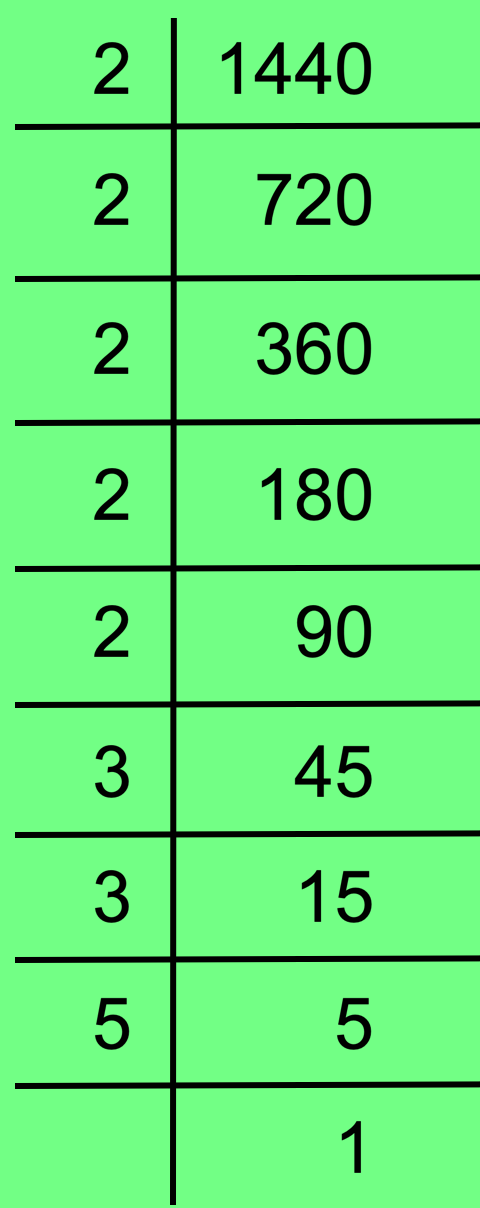
وبالتالي فإن 1440 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5
19. أوجد التحليل الأولي للعدد 5040 باستخدام طريقة القسمة.
حل:
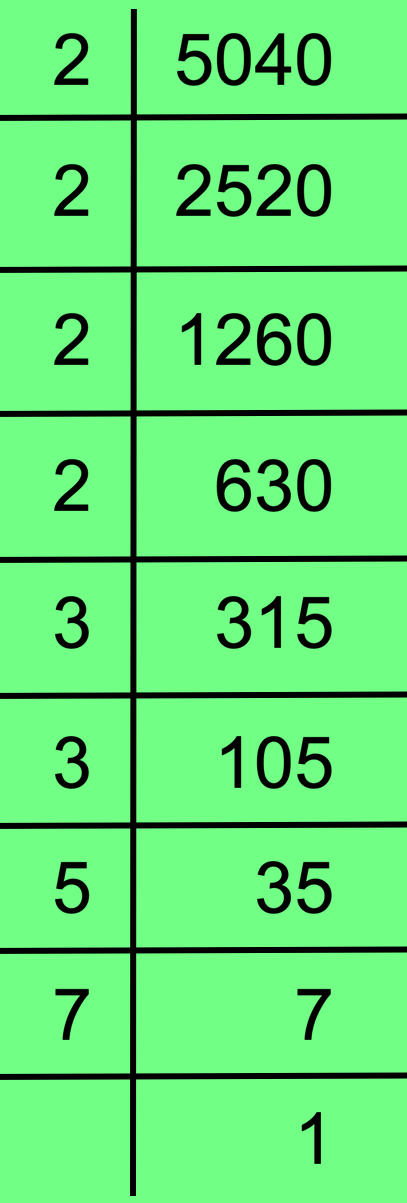
وبالتالي فإن 5040 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 7
خاصية التخصيم الأولي:
دعونا نوجد العوامل الأولية للعدد 36 بطريقة شجرة العوامل.
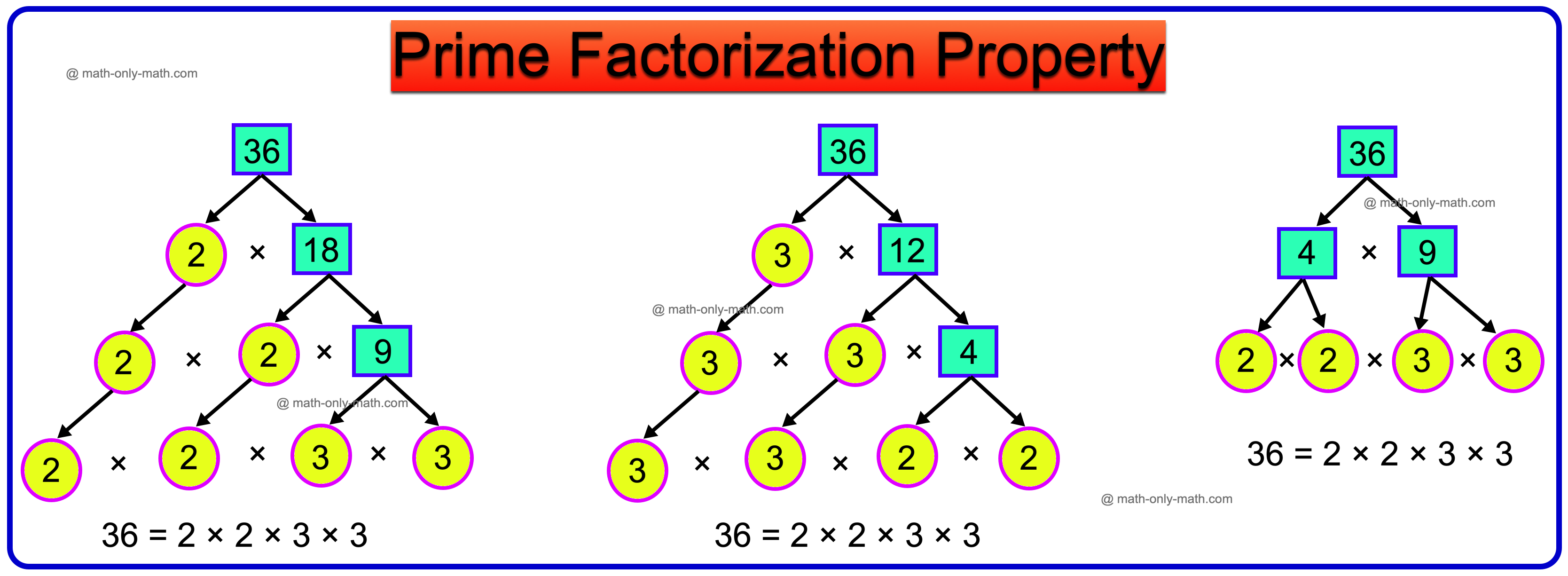
مما سبق نلاحظ أن العوامل الأولية للعدد 36 هي نفسها في أي طريقة من طرق شجرة العوامل باستثناء ترتيبها. ومن ثم، فإن التحليل الأولي للعدد 36 هو أمر فريد. تسمى هذه الخاصية خاصية التحليل الأولي أو النظرية الأساسية في الحساب. تنص على أن:
يمكن تحليل كل عدد مركب إلى عوامل أولية بطريقة واحدة فقط، باستثناء ترتيب العوامل الأولية.
الأسئلة المتداولة حول التخصيم الأولي:
1. ما هو التخصيم الأولي؟
التحليل هو عملية يتم من خلالها تقسيم عدد صحيح (تحليله) إلى عوامل، وإذا كان كل عامل عددًا أوليًا، فإن هذا التخصيم من رقم يسمى أولي التخصيم.
2. رئيس الوزراء التخصيم 30 هو
(ط) 2 × 15؛ (ثانيا) 5 × 6؛ (ثالثا) 6 × 5؛ (رابعا) 2 × 3 × 5
حل:
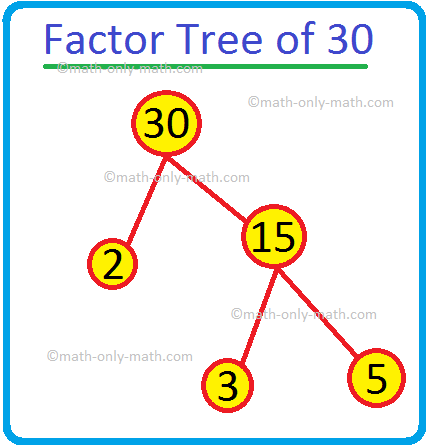
30 = 2 × 3 × 5
وبالتالي فإن الخيار (رابعا) هو الإجابة الصحيحة.
3. أوجد التحليل الأولي للعدد 24 باستخدام طريقة القسمة.
حل:

ومن ثم، فإن التحليل الأولي للعدد 24 = 2 × 2 × 2 × 3.
ورقة عمل حول التحليل الأولي:
I. أوجد العوامل الأولية للرقم المحدد من خلال التحليل الأولي. يظهر الأول كمثال لك.
(ط) 144
(ثانيا) 81
(ثالثا) 72
(رابعا) 48
(ت) 100
(السادس) 64
(السابع) 108
(الثامن) 248
(التاسع) 256
إجابة:
تسمى طريقة إيجاد جميع العوامل الأولية لعدد ما بالتحليل الأولي.
إجابة:
لإيجاد العوامل الأولية لعدد صحيح، نستخدم اختبارات قابلية القسمة. يمكننا قسمة العدد على التوالي على الأعداد الأولية 2، 3، 5، 7 وهكذا حتى يصبح المقسوم 1 والتعبير عنها كحاصل ضرب الأعداد الأولية. تُعرف هذه الطريقة بطريقة التقسيم. هناك طريقة أخرى تُعرف باسم طريقة شجرة العوامل. تُفضل طريقة شجرة العوامل بشكل عام عندما يكون العدد كبيرًا.
● عوامل.
● العوامل المشتركة.
● العامل الرئيسي.
● العوامل الأولية المتكررة
● العامل المشترك الأعلى (HCF).
● أمثلة على العامل المشترك الأعلى (HCF).
● العامل المشترك الأكبر (GCF).
● أمثلة على العامل المشترك الأكبر (GCF).
● التخصيم الأولي.
● إيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي.
● أمثلة لإيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي.
● إيجاد العامل المشترك الأعلى باستخدام طريقة القسمة
● أمثلة لإيجاد العامل المشترك الأعلى لعددين باستخدام طريقة القسمة.
● إيجاد العامل المشترك الأعلى لثلاثة أرقام باستخدام طريقة القسمة.
صفحة أرقام الصف الخامس
مسائل الرياضيات للصف الخامس
من التخصيم الأولي إلى الصفحة الرئيسية
لم تجد ما كنت تبحث عنه؟ أو تريد معرفة المزيد من المعلومات عنها الرياضيات فقط الرياضيات.
استخدم بحث Google هذا للعثور على ما تحتاجه.
اشترك في النشرة البريدية ليصلك كل جديد.





