السحر المربع | أضف ما يصل إلى 15 | أضف ما يصل إلى 27 | تسلسل فيبوناتشي
مدونة ضوء التعليمية تقدم لكم درس “السحر المربع | أضف ما يصل إلى 15 | أضف ما يصل إلى 27 | تسلسل فيبوناتشي
” نترككم مع المقال:
في مربع سحري ، يضيف كل صف وعمود وكل من الأقطار إلى نفس المجموع.
هنا ميدان سحري. يتم وضع الأرقام من 1 إلى 9 في المربعات الصغيرة بطريقة لا يتم تكرار أي رقم ويساوي مجموع الأرقام الثلاثة عمودًا ، وحكيماً ، ويساوي 15.
هذا هو 3 × 3 ميدان سحري.
أ. هذا هو ميدان سحري.
جميع الصفوف الثلاثة تضيف حتى 15.
جميع الأعمدة الثلاثة تضيف ما يصل إلى 15.
الأقطار 2 يضيف ما يصل إلى 15.
هناك 8 خطوط ، كل 15 خطوط.
في هذا المربع السحري ، يتم استخدام الأرقام من 1 إلى 9. في أحد هذه السطور ، تزيد الأرقام بمقدار 1.
القطري هو 4 ، 5 ، 6.
انظر بعناية وابحث في أي خط يزداد الأرقام بمقدار (أ) 2 (ب) 3
المربعات السحرية مماثلة مصنوعة أيضا.

Square Square (3 × 3) SUM = 15 فيديو
https://www.youtube.com/watch؟v=5HifemDmng4
هناك أمثلة على المربعات السحرية التي تشكلتها الأرقام 5 و 6 و 7 و 8 و 9 و 10 و 11 و 12 و 13 التي تتمتع بمجموع قطري وحكيمة من الأعمدة 27


في نفس النمط يمكن تشكيل المربعات السحرية الأخرى.
(ط) الأرقام 2 ، 3 ، 4 ، 5 ، 6 ، 7 ، 8 ، 9 و 10 ، مجموع = 18
(2) الأرقام تتراوح من 3 إلى 11 ومبلغ = 21
(3) الأرقام تتراوح من 4 إلى 12
(4) الأرقام تتراوح من 6 إلى 14 ومبلغ = 30
(5) الأرقام تتراوح من 7 إلى 15 ومبلغ = 33
(6) الأرقام تتراوح من 8 إلى 16 ومبلغ = 36
(السابع) الأرقام تتراوح من 9 إلى 17 ومبلغ = 39
قد يتم صنع المربعات السحرية التي تحتوي على 4 صفوف أو أكثر من الأعمدة.
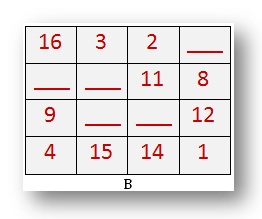
ب. هذا هو 4 من 4 سحر مربع. اكتشف الأرقام المفقودة. ماذا يضيف كل سطر ما يصل إلى؟
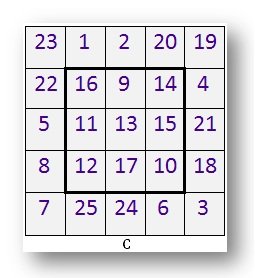
جيم هذا هو 5 × 5 ميدان سحري.
لديها 5 صفوف و 5 أعمدة.
اكتشف إجمالي الخط.
تحقق مما إذا كان كل من الصفوف الخمسة و 5 أعمدة و 2 أقطار يضيفون إلى نفس الرقم.
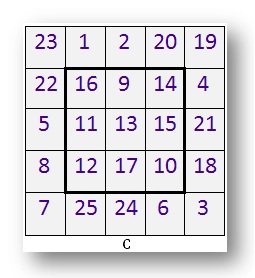
في وسط هذا 5 من 5 ميدان سحري هو 3 في 3 مربع. ارسم هذا 3 في 3 مربع على ورقة.
انسخ الرقم في كل مربع.
هل هذا 3 في 3 مربع أ ميدان سحري؟
ما هو إجمالي خط كل صف وعمود؟
ما هو مجموع الأقطار؟ هل تزداد الأرقام بمقدار 1 في أي من الخطوط؟ لون هذا الخط.
استخدم ألوانًا مختلفة لتظليل الخطوط حيث تزداد الأرقام بمقدار (أ) 2 (ب) 3.
د. هذا هو 6 × 6 سحر المربع.
ابحث عن إجمالي الخط.
تحقق من أن بعض الصفوف والأعمدة تضيف إلى هذا الرقم.
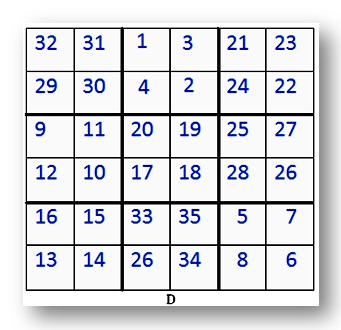
لاحظ أن الخطوط السميكة تقسم المربع إلى 9 مربعات أصغر.
كل مربع صغير لديه 4 أرقام.
ماذا تلاحظ عن الأرقام الأربعة في كل من هذا المربع الصغير؟
أضف ما يصل إلى 4 أرقام في كل من المربعات التسعة.
اكتب إجابتك في 3 إلى 3 مربع.
تم إجراء أول مربعين من أجلك.
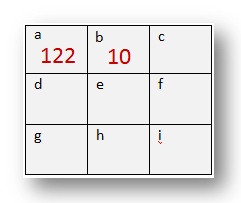
(أ) 29 + 30 + 31 + 32 = 122
(ب) 1 + 2 + 3 + 4 = 10
(ج) 21 + 22 +23 + 24 = ____
(د) 9 + 10 + 11 + 12 = ____
(هـ) 17 + 18 + 19 + 20 = ____
(و) 25 + 26 + 27 + 28 = ____
(ز) 13 + 14 + 15 + 16 = ____
(H) 33 + 34 + 35 + 26 = ____
(ط) 5 + 6 + 7 + 8 = ____
أضف الآن الأرقام في كل صف ، عمود ، قطري ، وأكد أن هذا أيضًا مربع سحري!
راقب نمط العدد
1 ∙ 1 ∙ 2 ∙ 3 ∙ 5 ∙ 8 ∙ 13 ∙ 21 ∙ 34
كل رقم بعد الرقم الثاني يساوي مجموع الرقمين السابقتين.
يسمى هذا النوع من العلاقة تسلسل فيبوناتشي. تم تطويره بواسطة ليوناردو فيبوناتشي من إيطاليا على مدار عام 1200.
يمكننا مراقبة الأرقام من تسلسل فيبوناتشي في أماكن مختلفة في الطبيعة ؛ بتلات من الزهور أوراق النباتات مقاييس الأناناس والعقد من مخروط الصنوبر.
راقب نمط العدد
1 ∙ 3 ∙ 6 ∙ 10 ∙ 15 ∙ 21
يتكون تسلسل الأرقام هذا رقم الثلاثي.
يبدأ التسلسل بـ 1. ثم
1 + 2 = 3
3 + 3 = 6
6 + 4 = 10
10 + 5 = 15
15 + 6 = 21
هناك حقيقة أخرى مثيرة للاهتمام.
يمكنك الحصول على عدد من 3 أرقام مثل 356.
إذا كتبنا بعد ذلك نفس العدد من ثلاثة أرقام ، نحصل على 356356.
هذا الرقم مقسم على 7 و 11 و 13.
479479 مقسوم أيضًا على 7 و 11 و 13.
وبالمثل ، قد يتم تقديم أرقام أخرى والتي يمكن تقسيمها على 7 و 11 و 13.
مفهوم ذات صلة
● الأنماط والرياضيات العقلية
● حساب الأرقام في النمط المناسب
● أنماط الأرقام الفردية
● ثلاثة أرقام متتالية
● الرقم الذي شكله أي قوة
● نتاج الرقم
● ميدان السحر
● مربع رقم
● اختلاف المربعات
● مضروبة في حد ذاتها
● لغز
● أنماط
● أنظمة العد
أنشطة الرياضيات الصف الرابع
من Magic Square إلى الصفحة الرئيسية
لم تجد ما كنت تبحث عنه؟ أو تريد معرفة المزيد من المعلومات حول الرياضيات فقط الرياضيات.
استخدم بحث Google هذا للعثور على ما تحتاجه.
اشترك في النشرة البريدية ليصلك كل جديد.





