الكسر كقسمة |يمكن التعبير عن الكسور بقسمة |كسر

يُعرف الكسر كقسمة أيضًا باسم الكسر كحاصل.

هل يمكنك قسمة عدد أصغر على عدد أكبر؟

لقد تعلمنا كيفية قسمة عدد أكبر على عدد أصغر.

نحن نعلم أن 12 ÷ 4 = 3.

إذا كان لديك 12 قطعة شوكولاتة وتم توزيعها بالتساوي على 4 أطفال، فإن كل واحد منهم يحصل على 3 قطع شوكولاتة. إذا تم توزيع 8 قطع شوكولاتة على 4 أطفال، فإن نصيب كل واحد هو 2 قطعة شوكولاتة، لأن 842. عندما نوزع 4 قطع شوكولاتة بالتساوي على 4 أطفال، فإن كل واحد يحصل على قطعة شوكولاتة واحدة.

ماذا تلاحظ من هذا؟ عدد الأطفال هو نفسه، ولكن عدد الشوكولاتة آخذ في التناقص. وأيضاً عندما يتناقص عدد الشوكولاتة فإن حصة كل قطعة منها تتناقص.

هنا، لا يحصل أي طفل على قطعة شوكولاتة كاملة، بل يحصل كل طفل على جزء فقط من قطعة شوكولاتة كاملة. حصة كل جزء هي \(\frac{1}{4}\)، حيث أن هناك أربعة أجزاء متساوية ويحصل كل جزء على جزء واحد.

\(\frac{1}{4}\) هي النتيجة التي تم الحصول عليها عندما 1 مقسوم على 4.

دعونا نفكر في موقف آخر، حيث يوجد 3 قطع شوكولاتة في علبة ويجب توزيع هذه الشوكولاتة بالتساوي على 4 أطفال.

ويمكن القيام بذلك بالطريقة التالية:

1. قسمي كل قطعة من الشوكولاتة الثلاث إلى 4 أجزاء متساوية.

2. قم بإحصاء إجمالي عدد الأجزاء (القطع) التي تم الحصول عليها، هنا 12 جزءًا.

3. قم بتقسيم هذه الأجزاء الـ 12 على 4 أطفال بالتساوي.

4. يحصل كل طفل على 3 أجزاء بعد القسمة، أي 3 أجزاء من 4 قطع من الشوكولاتة. بمعنى آخر، يحصل كل طفل على 3/4 قطعة من الشوكولاتة.

والآن يتم تمثيل الوصف أعلاه في شكل جدول على النحو التالي:

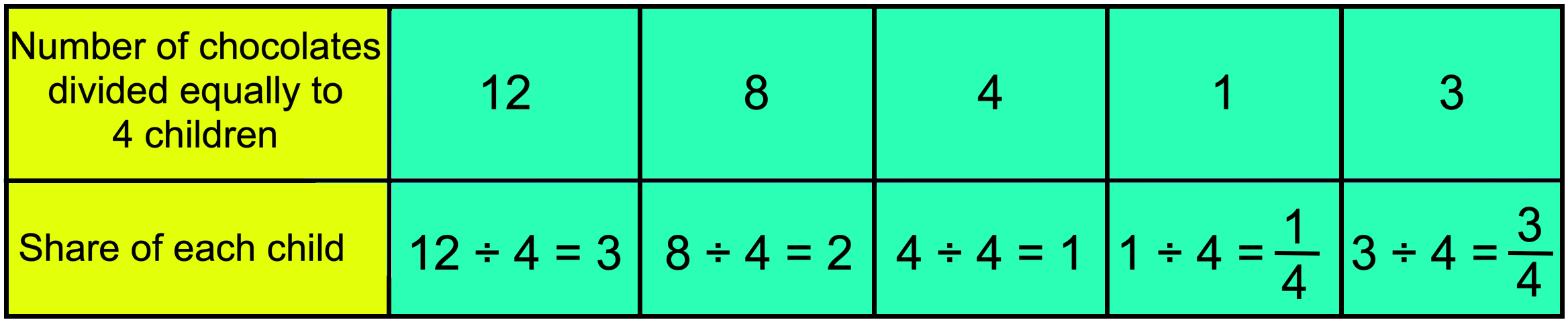
والآن يمكننا القول إنه من الممكن قسمة عدد أصغر على عدد أكبر. والنتيجة في هذه الحالات ليست عددا صحيحا، بل هي مجرد جزء من الكل أو الكسر.

لذا، \(\frac{1}{4}\) هو نفسه 1 ÷ 4،

\(\frac{3}{4}\) هو نفسه 3 ÷ 4.

أمثلة على الكسر كقسمة

إذا تم توزيع 8 قطع بسكويت بين طفلين بالتساوي، فسيحصل كل منهم على 8 ÷ 2 = 4 قطع بسكويت.

إذا تم توزيع 4 قطع بسكويت بين طفلين بالتساوي، فسيحصل كل منهم على 4 ÷ 2 = 2 بسكويت.

إذا تم تقسيم قطعة بسكويت واحدة بين طفلين بالتساوي، فسيحصل كل واحد منهم على نصف (1 ÷ 2) بسكويت.

بصورة مماثلة،

إذا تم توزيع 5 تفاحات بين طفلين بالتساوي، فسيحصل كل واحد على 5 ÷ 2 أو 5/2 تفاحة.

على سبيل المثال، يمكن التعبير عن الأقسام على شكل كسور.

(ط) 8 ÷ 2 = 8/2؛

(ب) 12 ÷ 4 = 12/4

(ثالثًا) 5 ÷ 3 = 5/3

(رابعا) 15 ÷ 5 = 15/5

(ت) 11 ÷ 19 = 11/19

(6) إذا كان لدى صوفي 3 قطع من البسكويت وأرادت إعطاء حصة متساوية لراشيل، فما هي الحصة التي سيحصل عليها كل منهما؟ نقسم 3 على 2. وهو مكتوب على شكل كسر \(\frac{3}{2}\).

1. على سبيل المثال يمكن التعبير عن الكسور بالقسمة.

(ط) 9/7 = 9 ÷ 7

(2) 3/11 = 3 ÷ 11

(ثالثًا) 90/63 = 90 ÷ 63

(رابعا) 1/5 = 1 ÷ 5

(ت) 14/17 = 14 ÷ 17

2. عبر عن كل من الكسور التالية بالقسمة:

(ط) \(\frac{1}{7}\)

(ثانيا) \(\frac{3}{8}\)

(ثالثًا) \(\frac{11}{15}\)

حل:

(ط) \(\frac{1}{7}\) = 1 ÷ 7

(2) \(\frac{3}{8}\) = 3 ÷ 8

(ثالثًا) \(\frac{11}{15}\) = 11 ÷ 15

● جزء

صفحة الأرقام

صفحة الصف السادس

من الكسر كقسمة إلى الصفحة الرئيسية