إيجاد العامل المشترك الأعلى باستخدام طريقة القسمة

مدونة ضوء التعليمية تقدم لكم درس “إيجاد العامل المشترك الأعلى باستخدام طريقة القسمة
” نترككم مع المقال:
اشترك في موقعنا ◀️ قناة يوتيوب 🔴 للحصول على أحدث مقاطع الفيديو والتحديثات والنصائح.
للعثور على العامل المشترك الأكبر باستخدام طريقة القسمة تمت مناقشته هنا.
إن العثور على العامل المشترك الأكبر (HCF) عن طريق التحليل الأولي لعدد كبير ليس أمرًا مريحًا للغاية. تعتبر طريقة القسمة المطولة أكثر فائدة للأعداد الكبيرة.
في هذه الطريقة نقوم أولا بقسمة العدد الأكبر على العدد الأصغر. ويصبح الباقي هو المقسوم عليه الجديد والمقسوم عليه السابق هو المقسوم الجديد. نواصل العملية حتى نحصل على 0 الباقي.
نستخدم طريقة القسمة المتكررة لإيجاد العامل المشترك الأكبر (HCF) لعددين أو أكثر.
لإيجاد العامل المشترك الأكبر باستخدام طريقة القسمة نتبع الخطوات التالية:
الخطوة الأولى: قسمة العدد الكبير على الأصغر.
الخطوة الثانية: ثم يتم التعامل مع الباقي كمقسوم والمقسوم عليه كأرباح.
الخطوة الثالثة: قسمة المقسوم عليه الأول على الباقي الأول.
الخطوة الرابعة:قسمة المقسوم عليه الثاني على الباقي الثاني.
الخطوة الخامسة: استمر في هذه العملية حتى يصبح الباقي 0.
الخطوة السادسة: المقسوم عليه الذي لا يترك باقيًا هو HCF أو GCD للرقمين، وبالتالي فإن المقسوم عليه الأخير هو العامل المشترك الأعلى المطلوب (HCF) للأرقام المحددة.
دعونا نفكر في بعض الأمثلة لإيجاد العامل المشترك الأكبر (HCF) باستخدام طريقة القسمة.
1. أوجد العامل المشترك الأكبر (HCF) للعددين 18 و30 باستخدام طريقة القسمة.
حل:
الخطوة الأولى: هنا علينا قسمة 30 على 18.
[Divide the larger number by the smaller one].
الخطوة الثانية: المقسوم عليه الأول هو 18 والباقي هو 12، لذا علينا قسمة 18 على 12.
[Divide the first divisor by the first remainder].
الخطوة الثالثة: الآن قم بتقسيم المقسوم عليه الثاني 12 على الباقي الثاني 6.
[Divide the second divisor by the second remainder].
الخطوة الرابعة: والباقي يصبح 0
الخطوة الخامسة: لذلك، العامل المشترك الأكبر = 6.
[The last divisor is the required highest common factor (H.C.F) of the given numbers].
2. أوجد العامل المشترك الأكبر (HCF) للعددين 75 و180 باستخدام طريقة القسمة.
حل:
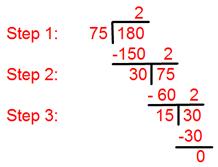
الخطوة الأولى: علينا هنا قسمة 180 على 75.
[Divide the larger number by the smaller one].
الخطوة الثانية: المقسوم عليه الأول هو 75 والباقي 30، لذا علينا قسمة 75 على 30.
[Divide the first divisor by the first remainder].
الخطوة الثالثة: الآن قم بتقسيم المقسوم عليه الثاني 30 على الباقي الثاني 15.
[Divide the second divisor by the second remainder].
الخطوة الرابعة: والباقي يصبح 0
الخطوة الخامسة: لذلك، العامل المشترك الأكبر = 15.
[The last divisor is the required highest common factor (H.C.F) of the given numbers].
3. أوجد HCF للعددين 112 و144 بطريقة القسمة المطولة.
حل:

اقسم 144 على 112
اقسم 112 على الباقي 32
اقسم 32 على الباقي 16
والآن الباقي 0
ومن ثم، فإن HCF 112 و144 هو 16
4. كيفية العثور على العامل المشترك الأعلى (HCF) للعددين 1225 و875 باستخدام طريقة القسمة المطولة؟
حل:

والباقي صفر
وبالتالي، فإن HCF من 1225 و 875 هو المقسوم الأخير، أي، 175.
كيفية العثور على HCF لثلاثة أرقام باستخدام طريقة القسمة المطولة؟
5. كيف يمكن إيجاد العامل المشترك الأعلى لثلاثة أرقام 36 و96 و128 باستخدام طريقة القسمة؟
حل:

أولًا، نوجد HCF للعددين 36 و96، ثم HCF لنتيجتهما و128.
اقسم 96 على 36 واحصل على الباقي 24.
الآن، اقسم 36 على 24 واحصل على الباقي 12.
ثم اقسم 24 على 12 واحصل على الباقي 0.
المقسوم الأخير في هذه العملية هو 12.
ومن ثم، فإن HCF لـ 36 و96 هو 12.
والآن، نوجد HCF للعددين 12 و128.
المقسوم الأخير هو 4.
ومن ثم، فإن العامل المشترك الأعلى (hcf) هو 36 و96 و128 4.
6. أوجد HCF للأعداد 216 و468 و828 بطريقة القسمة.
حل:
الخطوة 1: سنجد أولاً HCF بقيمة 216 و828

الخطوة 2: الآن أوجد HCF بقيمة 36 و468.
ومن ثم، فإن HCF للأرقام 216 و468 و828 هو 36
HCF بطريقة القسمة المطولة:
في HCF بطريقة القسمة المطولة، نقوم أولاً بقسمة العدد الأكبر على الرقم الأصغر ثم نقسم العدد الأصغر على الباقي. نواصل العملية حتى نحصل على 0 الباقي.
المقسوم عليه هو HCF للأرقام المعطاة.
على سبيل المثال:
7. أوجد HCF للعددين 318 و504 بطريقة القسمة المطولة.
 | اقسم 504 على 318. اقسم 318 على الباقي 186. اقسم 186 على الباقي 132. اقسم 132 على الباقي 54. اقسم 54 على الباقي 24. قسمة 24 على الباقي 6 والآن الباقي 0 لذا، لا يمكننا أن ننقسم أكثر. |
وبالتالي، 6 هو HCF لـ 318 و514.
● عوامل.
● العوامل المشتركة.
● العامل الرئيسي.
● العوامل الأولية المتكررة
● العامل المشترك الأعلى (HCF).
● أمثلة على العامل المشترك الأعلى (HCF).
● العامل المشترك الأكبر (GCF).
● أمثلة على العامل المشترك الأكبر (GCF).
● التخصيم الأولي.
● إيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي.
● أمثلة لإيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي.
● إيجاد العامل المشترك الأعلى باستخدام طريقة القسمة
● أمثلة لإيجاد العامل المشترك الأعلى لعددين باستخدام طريقة القسمة.
● إيجاد العامل المشترك الأعلى لثلاثة أرقام باستخدام طريقة القسمة.
صفحة أرقام الصف الخامس
مسائل الرياضيات للصف الخامس
من للعثور على العامل المشترك الأعلى باستخدام طريقة القسمة إلى الصفحة الرئيسية
لم تجد ما كنت تبحث عنه؟ أو تريد معرفة المزيد من المعلومات عنها الرياضيات فقط الرياضيات.
استخدم بحث Google هذا للعثور على ما تحتاجه.
اشترك في النشرة البريدية ليصلك كل جديد.





