إيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي

للعثور على العامل المشترك الأعلى باستخدام طريقة التحليل الأولي تمت مناقشته هنا.

الخطوة الأولى:

أوجد التحليل الأولي لكل عدد من الأعداد المعطاة.

الخطوة الثانية:

حاصل ضرب جميع العوامل الأولية المشتركة هو HCF للأرقام المعطاة.

دعونا نفكر في بعض الأمثلة لإيجاد العامل المشترك الأكبر باستخدام طريقة التحليل الأولي.

1. أوجد العامل المشترك الأكبر (HCF) للعددين 14 و8 باستخدام طريقة التحليل الأولي.

حل:

14 = 1 × 2 × 7.

8 = 1 × 2 × 2 × 2.

العامل المشترك 8 و 14 = 1 و 2.

HCF هو نتاج القوى الأدنى للعوامل المشتركة بين جميع الأرقام.

العامل المشترك الأعلى 8 و 14 = 2.

2. أوجد العامل المشترك الأكبر (HCF) للعددين 9 و27 باستخدام طريقة التحليل الأولي.

حل:

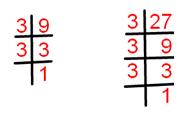
9 = 1 × 3 × 3.

27 = 1 × 3 × 3 × 3.

العامل المشترك 9 و 27 = 1 و 3 و 3.

العامل المشترك الأعلى 9 و 27 = 3 × 3 = 9.

3. أوجد العامل المشترك الأكبر (HCF) للعددين 6 و16 باستخدام طريقة التحليل الأولي.

حل:

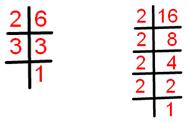
6 = 1 × 2 × 3.

16 = 1 × 2 × 2 × 2 × 2.

العامل المشترك 6 و 16 = 2.

العامل المشترك الأعلى 6 و 16 = 2.

4. أوجد العامل المشترك الأكبر (HCF) للعددين 18 و24 باستخدام طريقة التحليل الأولي.

حل:

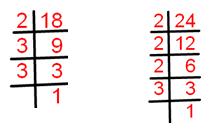
18 = 1 × 2 × 3 × 3.

24 = 1 × 2 × 2 × 2 × 3.

العامل المشترك 18 و 24 = 1، 2، 3.

العامل المشترك الأعلى 18 و 24 = 2 × 3 = 6.

5. أوجد العامل المشترك الأعلى (HCF) للعددين 12 و56 باستخدام طريقة التحليل الأولي.

حل:

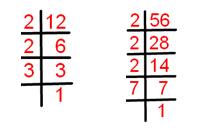
12 = 1 × 2 × 2 × 3.

56 = 1 × 2 × 2 × 2 × 7.

العامل المشترك 12 و 56 = 1، 2، 2.

العامل المشترك الأعلى 12 و 56 = 2 × 2 = 4.

6. أوجد HCF لـ 108 و132 بطريقة التحليل الأولي.

حل:

108 = 2 × 2 × 3 × 3 × 3

132 = 2 × 2 × 3 × 11

وبالتالي فإن HCF هو 2 × 2 × 3 = 12

ورقة عمل على HCF باستخدام طريقة التحليل الأولي:

1. حدد HCF للأعداد التالية بطريقة التحليل الأولي:

(ط) 42، 56

(ثانيا) 24، 72

(ثالثًا) 39، 52

(رابعا) 44، 77

(ت) 345، 506

(السادس) 69، 253

إجابة:

1. (ط) 14

(الثاني) 24

(ثالثا) 13

(رابعا) 11

(ت) 23

(السادس) 23

● عوامل.

● العوامل المشتركة.

● العامل الرئيسي.

● العوامل الأولية المتكررة

● العامل المشترك الأعلى (HCF).

● أمثلة على العامل المشترك الأعلى (HCF).

● العامل المشترك الأكبر (GCF).

● أمثلة على العامل المشترك الأكبر (GCF).

● التخصيم الأولي.

● إيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي.

● أمثلة لإيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي.

● إيجاد العامل المشترك الأعلى باستخدام طريقة القسمة

● أمثلة لإيجاد العامل المشترك الأعلى لعددين باستخدام طريقة القسمة.

● إيجاد العامل المشترك الأعلى لثلاثة أرقام باستخدام طريقة القسمة.

صفحة أرقام الصف الخامس

مسائل الرياضيات للصف الخامس

من للعثور على العامل المشترك الأعلى باستخدام طريقة التحليل الأولي إلى الصفحة الرئيسية