مدونة ضوء التعليمية تقدم لكم درس “إيجاد المضاعف المشترك الأصغر باستخدام طريقة التحليل الأولي
” نترككم مع المقال:
اشترك في موقعنا ◀️ قناة يوتيوب 🔴 للحصول على أحدث مقاطع الفيديو والتحديثات والنصائح.
للعثور على المضاعف المشترك الأصغر باستخدام طريقة التحليل الأولي تمت مناقشته هنا.
للعثور على المضاعف المشترك الأصغر لعددين أو أكثر، علينا أولاً إيجاد جميع العوامل الأولية للأرقام المعطاة وكتابتها واحدًا تحت الآخر. خذ عاملاً واحدًا من كل مجموعة عوامل مشتركة وابحث عن ناتجها. اضرب الناتج مع عوامل أخرى غير مجمعة. الناتج هو LCM من الأرقام المعطاة.
الخطوة الأولى: حل كل عدد معلوم إلى عوامله الأولية وعبر عن العوامل التي تم الحصول عليها في الصورة الأسية.
الخطوة الثانية: أوجد حاصل ضرب القوى الأعلى لجميع العوامل التي تحدث في أي من الأعداد المعطاة.
الخطوة الثالثة: المنتج الذي تم الحصول عليه في الخطوة الثانية هو المضاعف المشترك الأصغر (LCM) المطلوب.
على سبيل المثال:
1. أوجد المضاعف المشترك الأصغر (LCM) للعددين 9 و15 باستخدام طريقة التحليل الأولي.
حل:
الخطوة الأولى:
تحليل كل عدد إلى عوامله الأولية
9 = 3 × 3 = 3².
15 = 3 × 5.
الخطوة الثانية:
نتاج جميع العوامل ذات القوى العليا.
= 3^2 × 5 = 3 × 3 × 5 = 45.
الخطوة الثالثة:
المضاعف المشترك الأصغر المطلوب (LCM) 9 و15 = 45.
2. ما هو المضاعف المشترك الأصغر (LCM) للعددين 16 و 28 باستخدام طريقة التحليل الأولي؟
حل:
الخطوة الأولى:
تحليل كل عدد إلى عوامله الأولية
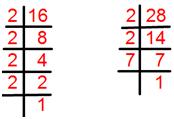
16 = 2 × 2 × 2 × 2 = 24.
28 = 2 × 2 × 7 = 22 × 7.
الخطوة الثانية:
نتاج جميع العوامل ذات القوى العليا.
= 24 × 7 = 2 × 2 × 2 × 2 × 7 = 112.
الخطوة الثالثة:
المضاعف المشترك الأصغر المطلوب (LCM) 16 و28 = 112.
3. أوجد المضاعف المشترك الأصغر للأعداد 32 و48 و72 عن طريق التحليل الأولي.
حل:
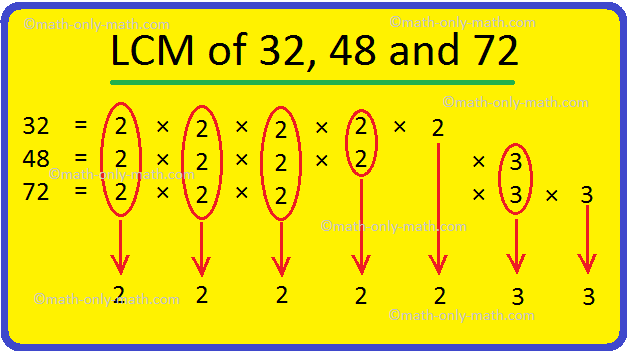
م م م 32، 48، 72 = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288.
4. أوجد المضاعف المشترك الأصغر لـ 24، 30 و54 بطريقة التحليل الأولي.
حل:
أولاً، أوجد العوامل الأولية لكل عدد.
العوامل الأولية للعدد 24 = 2 × 2 × 2 × 3
العوامل الأولية للعدد 30 = 2 × 3 × 5
العوامل الأولية للعدد 54 = 2 × 3 × 3 × 3
مما سبق نلاحظ أن 2 يحدث كعامل أولي كحد أقصى ثلاث مرات، و3 يحدث كعامل أولي كحد أقصى ثلاث مرات، و5 يحدث مرة واحدة فقط.
ومن ثم، فإن المضاعف المشترك الأصغر المطلوب هو 2 × 2 × 2 × 3 × 3 × 3 × 5 = 1080.
5. أوجد المضاعف المشترك الأصغر لـ 60، 70 و108 بطريقة التحليل الأولي.
حل:
أولاً، أوجد العوامل الأولية لكل عدد.
العوامل الأولية للعدد 60 = 2 × 2 × 3 × 5
العوامل الأولية للعدد 70 = 2 × 5 × 7
العوامل الأولية للعدد 108 = 2 × 2 × 3 × 3 × 3
مما سبق نلاحظ أن 2 يحدث كعامل أولي كحد أقصى مرتين، و3 يحدث كعامل أولي كحد أقصى ثلاث مرات، و5 و7 يحدثان مرة واحدة فقط.
ومن ثم، فإن المضاعف المشترك الأصغر المطلوب هو 2 × 2 × 3 × 3 × 3 × 5 × 7 = 3780.
● مضاعفات.
المضاعفات المشتركة.
المضاعف المشترك الأصغر (LCM).
إيجاد المضاعف المشترك الأصغر باستخدام طريقة التحليل الأولي.
أمثلة للعثور على المضاعف المشترك الأصغر باستخدام طريقة التحليل الأولي.
لإيجاد المضاعف المشترك الأصغر باستخدام طريقة القسمة
أمثلة للعثور على المضاعف المشترك الأصغر لعددين باستخدام طريقة القسمة
أمثلة للعثور على المضاعف المشترك الأصغر لثلاثة أرقام باستخدام طريقة القسمة
العلاقة بين HCF وLCM
ورقة عمل على HCF وLCM
مسائل كلامية على HCF وLCM
ورقة عمل عن المسائل الكلامية في HCF وLCM
صفحة أرقام الصف الخامس
مسائل الرياضيات للصف الخامس
من للعثور على المضاعف المشترك الأصغر باستخدام طريقة التحليل الأولي إلى الصفحة الرئيسية
لم تجد ما كنت تبحث عنه؟ أو تريد معرفة المزيد من المعلومات عنها الرياضيات فقط الرياضيات.
استخدم بحث Google هذا للعثور على ما تحتاجه.
اشترك في النشرة البريدية ليصلك كل جديد.
