الأعداد الزوجية والفردية بين 1 و100

مدونة ضوء التعليمية تقدم لكم درس “الأعداد الزوجية والفردية بين 1 و100
” نترككم مع المقال:

كل الأعداد الزوجية والفردية تتم مناقشة ما بين 1 و 100 هنا.

الأعداد الزوجية والفردية:

يقال إن شيئين يشتركان في نوع ما من العلاقة هما أزواج.

يمكن وضع بعض الكائنات في أزواج.

$أزواج من الرخام$

يمكن وضع 10 كرات في 5 أزواج.

لا يمكن وضع بعض الكائنات في أزواج.

$7 رخام$

لا يمكن وضع 7 كرات في أزواج.

تسمى الأرقام التي يمكن تجميعها في أزواج أرقامًا زوجية.

الأعداد مثل 2، 4، 6، 8، 10، 12، ….. هي حتى الأرقام.

الأعداد الزوجية تحتوي على الأرقام 0، 2، 4، 6 أو 8 في مكان الآحاد.

تسمى الأرقام التي لا يمكن تجميعها في أزواج أرقامًا فردية.

الأرقام مثل 1، 3، 5، 7، 9، 11، …. هي أرقام غريبة.

الأعداد الفردية لها الأرقام 1، 3، 5، 7، 9 في خانة الآحاد.

يتذكر:

• يمكن تجميع كافة الأرقام إما في أعداد فردية أو حتى في أعداد.

• يمكننا الحصول على عدد فردي بإضافة 1 إلى عدد زوجي والعكس صحيح.

الأرقام الزوجية:

العدد الذي يكون من مضاعفات العدد 2 يسمى رقما زوجيا.

أو

العدد زوجي إذا كان يقبل القسمة على 2 أو 2 يعتبر من عوامله.

وبالتالي فإن 2، 4، 6، 8، 10، 12، هي أرقام زوجية.

يتذكر

● الأرقام الزوجية تنتهي دائمًا بالأرقام 0، 2، 4، 6، 8.

● 2 هو أصغر عدد أولي وهو أيضًا العدد الأولي الزوجي الوحيد. جميع الأرقام الزوجية الأخرى مركبة

دعونا نرى المثال التالي للأرقام الزوجية:

تظهر أدناه 14 حبة قمح. دعونا نجعل أزواجهم.

$الأرقام الزوجية - حبات القمح$

يمكن إقران جميع الحبوب الـ 14. يتم استدعاء الأرقام التي يمكن إقرانها حتى أرقام. ومن ثم فإن 14 هو عدد زوجي.

بعض الأمثلة الأخرى للأعداد الزوجية هي 12 و24 و46 و68 و80.

أمثلة محلولة على الأعداد الزوجية:

1. اكتب جميع الأعداد الزوجية من 2 إلى 20.

حل:

جميع الأعداد الزوجية من 2 إلى 20 هي 2، 4، 6، 8، 10، 12، 14، 16، 18، 20.

الأرقام الفردية:

الرقم الذي ليس من مضاعفات العدد 2 يسمى رقما فرديا.

أو

يكون العدد فرديا إذا كان لا يقبل القسمة على 2.

وبالتالي فإن 1، 3، 5، 7، 9، 11، …. هي أرقام فردية.

أي عدد زوجي + 1 عدد فردي، أي إذا قسمنا أي عدد فردي على 2، نحصل على 1 كباقي.

يتذكر

● الأعداد الفردية تنتهي دائمًا بالأرقام 1، 3، 5، 7، 9.

دعونا نرى المثال التالي للأعداد الفردية:

الآن، انظر إلى 13 حبة من الذرة الموضحة أدناه. دعونا نحاول أن نجعل أزواجهم أيضًا.

$الأعداد الفردية - حبات الذرة$

لا يمكن إقران جميع الحبوب الـ 13. تسمى الأرقام التي لا يمكن إقرانها بالأرقام الفردية. وبالتالي فإن 13 هو عدد فردي.

بعض الأمثلة الأخرى للأعداد الفردية هي 11 و23 و55 و87 و99.

أمثلة محلولة على الأعداد الفردية:

1. أوجد جميع الأعداد الفردية من 1 إلى 17.

حل:

جميع الأعداد الفردية من 1 إلى 17 هي 1، 3، 5، 7، 9، 11، 13، 15، 17.

ما هي الأعداد الزوجية من 1 إلى 100؟

الأعداد الزوجية من 1 إلى 100 هي:

2 4 6 8 10

12 14 16 18 20

22 24 26 28 30

32 34 36 38 40

42 44 46 48 50

52 54 56 58 60

62 64 66 68 70

72 74 76 78 80

82 84 86 88 90

92 94 96 98 100

ما هي الأعداد الفردية من 1 إلى 100؟

الأعداد الفردية من 1 إلى 100 هي:

1 3 5 7 9

11 13 15 17 19

21 23 25 27 29

31 33 35 37 39

41 43 45 47 49

51 53 55 57 59

61 63 65 67 69

71 73 75 77 79

81 83 85 87 89

91 93 95 97 99

الأرقام الزوجية والفردية

$الأرقام الزوجية والفردية$

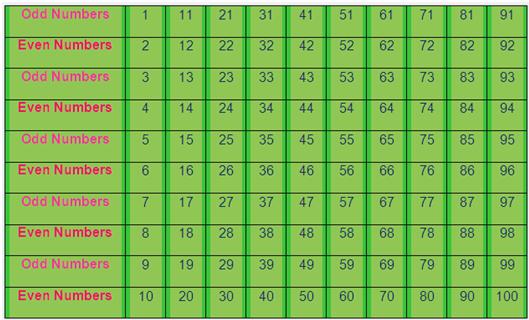
في الجدول التالي، الأرقام الغامقة هي أرقام زوجية والأرقام المتبقية هي أرقام جمع.

$الأعداد الزوجية والفردية بين 1 و100$

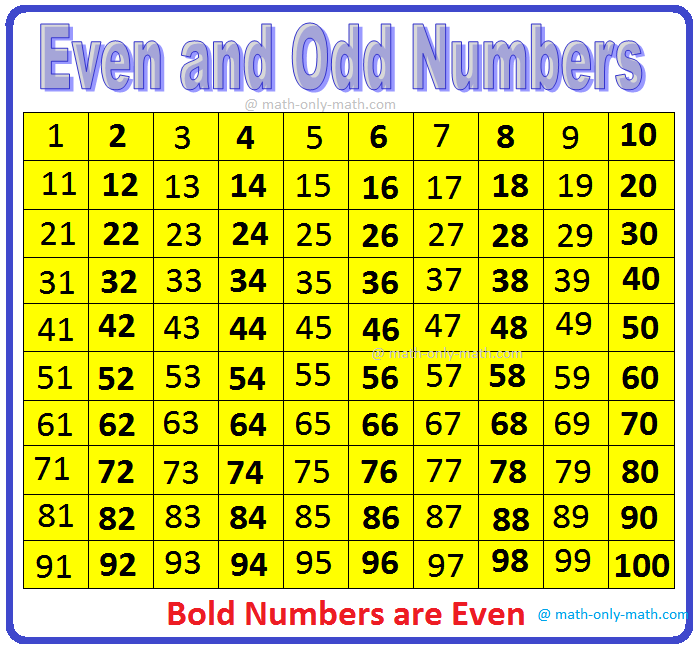
1. (ط) كل رقم يأتي بعد رقم زوجي هو عدد فردي

12 + 1 = 13

16 +1 = 17

176 + 1 = 177

216 + 1 = 217

(2) كل رقم يأتي بعد رقم فردي هو عدد زوجي

15 + 1 = 16

19 + 1 = 20

205 + 1 = 206

419 + 1 = 420

2. كل رقم له 2، 4، 6، 8 و0 في مكانه يقبل القسمة على 2، وبالتالي يكون رقمًا زوجيًا.

3. لا يوجد عدد يحتوي على 3، 5، 7، 9 في مكانه يقبل القسمة على 2 وبالتالي يكون رقم فردي.

4. جميع الأعداد الزوجية والفردية موجودة أعداد كاملة.

ورقة عمل حول الأعداد الزوجية والفردية:

1. اكتب جميع الأعداد الزوجية بين 35 و55.

إجابة:

36، 38، 40، 42، 44، 46، 48، 50، 52، 54.

2. أكتب كل الأعداد الفردية بين 40 و 70.

إجابة:

41، 43، 45، 47، 49، 51، 53، 55، 57، 59، 61، 63، 65، 67، 69.

3. اكتب ه حتى و يا للرقم الفردي في المربع.

(ط) 3 ▢

(ثانيا) 20 ▢

(ثالثا) 38 ▢

(رابعا) 69 ▢

(ت) 8 ▢

(السادس) 27 ▢

(السابع) 42 ▢

(ثامنا) 73 ▢

(التاسع) 9 ▢

(خ) 30 ▢

(الحادي عشر) 49 ▢

(الثاني عشر) 87 ▢

(الثالث عشر) 11 ▢

(الرابع عشر) 31 ▢

(الخامس عشر) 50 ▢

(السادس عشر) 90 ▢

(السابع عشر) 15 ▢

(الثامن عشر) 36 ▢

(التاسع عشر) 62 ▢

(xx) 99 ▢

إجابة:

3. (أنا) يا

(ثانيا) ه

(ثالثا) ه

(رابعا) يا

(ت) ه

(السادس) يا

(السابع) ه

(ثامنا) يا

(التاسع) يا

(خ) ه

(الحادي عشر) يا

(الثاني عشر) يا

(الثالث عشر) يا

(الرابع عشر) يا

(الخامس عشر) ه

(السادس عشر) ه

(السابع عشر) يا

(الثامن عشر) ه

(التاسع عشر) ه

(xx) يا

4. اكتب الرقم الزوجي التالي. لقد تم إنجاز واحد من أجلك:

(ط) 74 76

(ثانيا) 56 _____

(ثالثا) 86 _____

(رابعا) 98 _____

(ت) 42 _____

(السادس) 60 _____

إجابة:

4. (ثانيا) 58

(ثالثا) 88

(رابعا) 100

(ت) 44

(السادس) 62

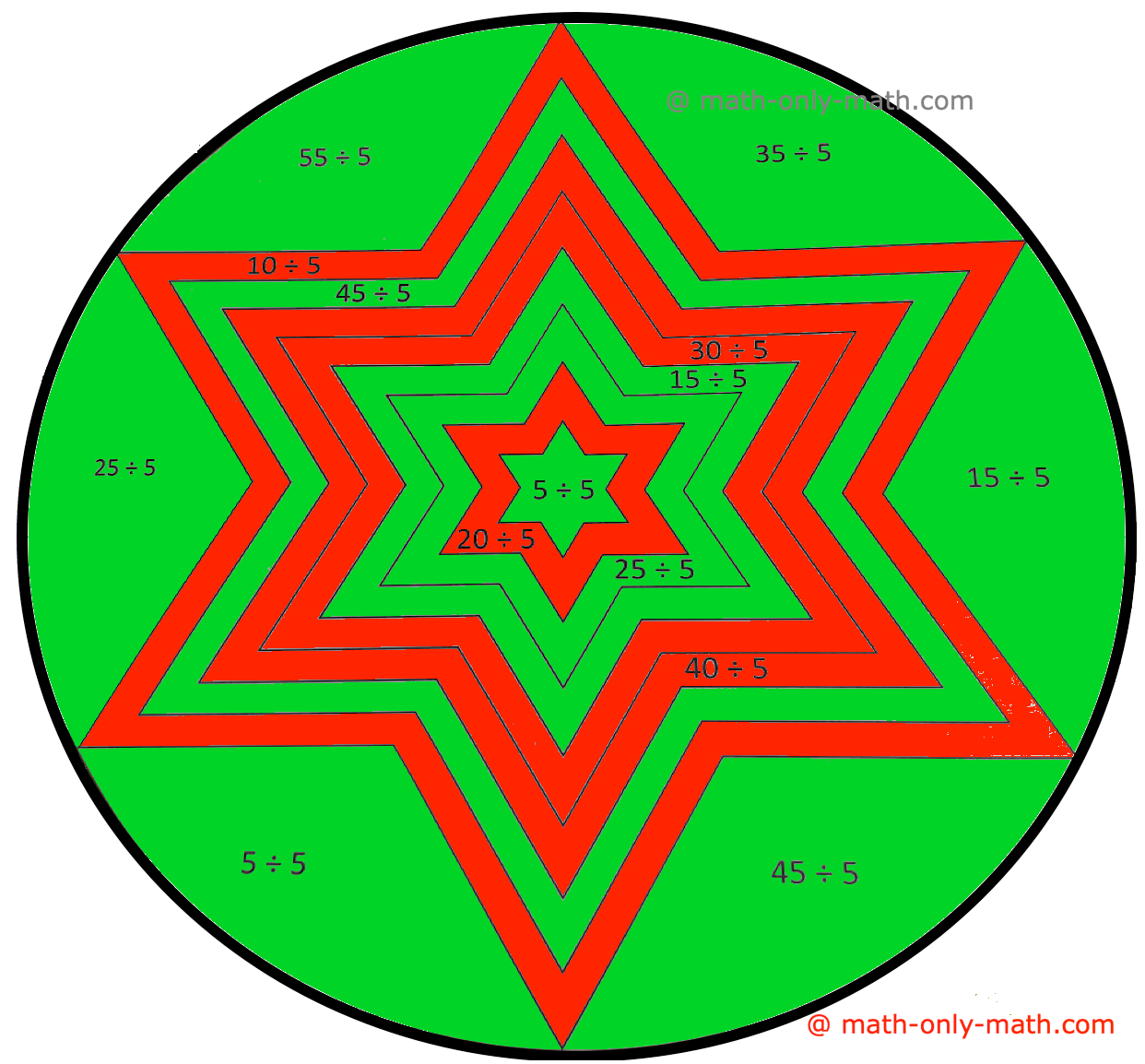
5. حل المبالغ. إذا كانت الإجابة زوجية، قم بتلوين الشكل أحمر. إذا كانت الإجابة غريبة، قم بتلوين الشكل أخضر:

$الأعداد الزوجية والأعداد الفردية$

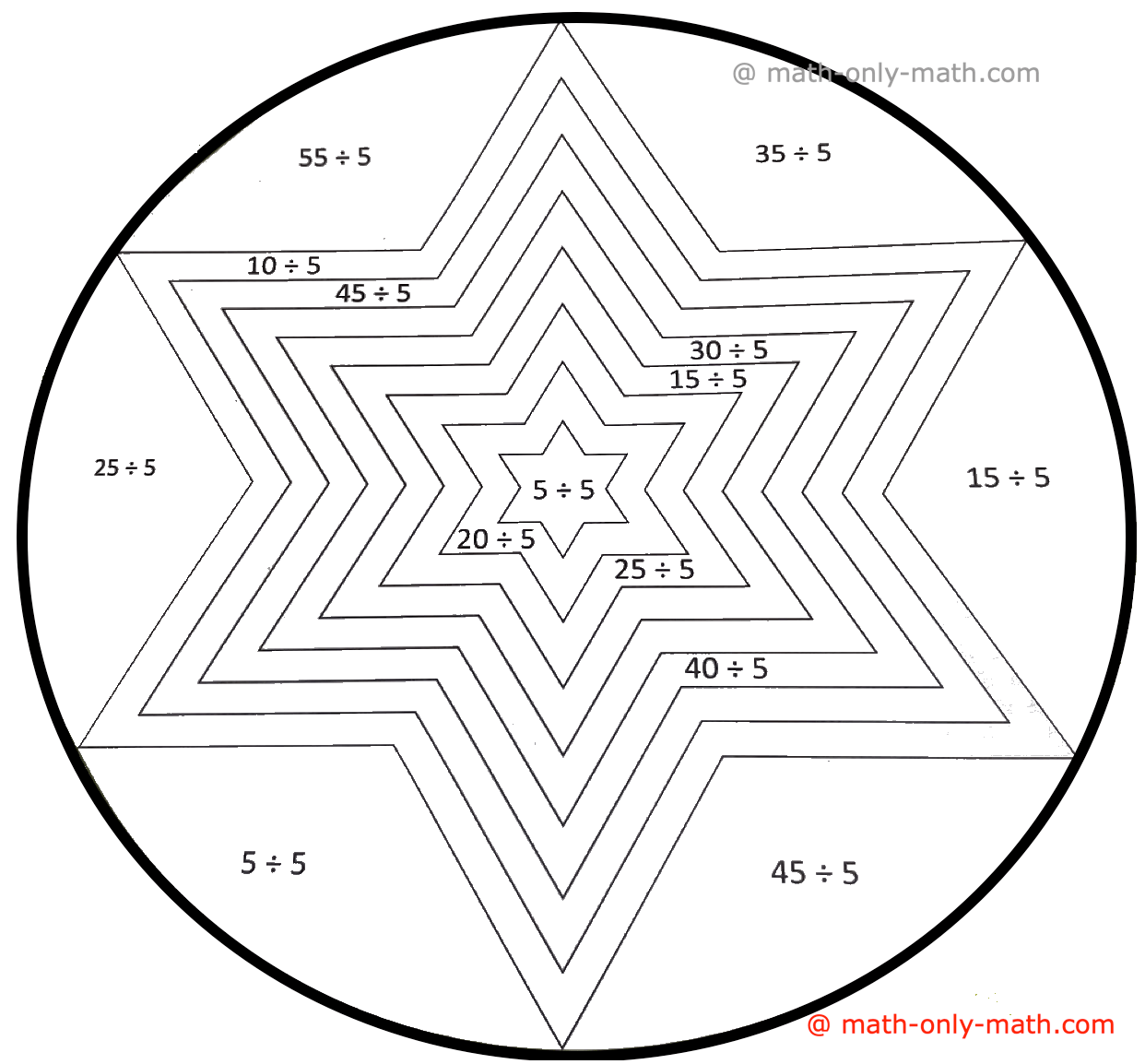
إجابة:

$مثال على الأرقام الزوجية والأرقام الفردية$

6. اكتب الرقم الفردي التالي. لقد تم إنجاز واحد من أجلك:

(ط) 51 53

(ثانيا) 65 _____

(ثالثا) 77 _____

(رابعا) 83 _____

(ت) 95 _____

(السادس) 55 _____

إجابة:

6. (ثانيا) 67

(ثالثا) 79

(رابعا) 85

(ت) 97

(السادس) 57

قد ترغب في هذه

$العامل المشترك الأعلى (HCF) لعددين أو أكثر هو العدد الأكبر الذي يقسم كل منهم بالضبط. الآن سوف نتعرف على طريقة إيجاد العامل المشترك الأعلى (HCF). الخطوات 1: ابحث عن جميع عوامل كل رقم محدد. الخطوة الثانية: إيجاد العوامل المشتركة لـ$
$التحليل الأولي أو التحليل الكامل للرقم المحدد هو التعبير عن رقم معين كحاصل ضرب العامل الأولي. عندما يتم التعبير عن عدد كحاصل ضرب عوامله الأولية، يطلق عليه اسم التحليل الأولي. على سبيل المثال، 6 = 2 × 3. لذا فإن 2 و3 عوامل أولية$
$وسنناقش هنا المضاعفات والعوامل وكيفية ارتباطها ببعضها البعض. عوامل الرقم هي تلك الأرقام التي يمكنها قسمة الرقم بالضبط. على سبيل المثال، 1 و 2 و 3 و 6 هي$
$يكون الرقم قابلاً للقسمة على 3، إذا كان مجموع أرقامه كلها من مضاعفات 3 أو قابلية القسمة على 3. فكر في الأرقام التالية لمعرفة ما إذا كانت الأرقام قابلة للقسمة على 3 أم لا: (i) 54 مجموع جميع الأرقام 54 = 5 + 4 = 9 وهو يقبل القسمة على 3.$
$يكون الرقم قابلاً للقسمة على 4 إذا كان الرقم مكونًا من أرقامه في مكان العشرة ومكان الوحدة (أي آخر رقمين في أقصى الجانب الأيمن منه) يقبل القسمة على 4. خذ بعين الاعتبار الأرقام التالية التي تقبل القسمة على 4 أو التي تقبل القسمة بحلول 4، وذلك باستخدام اختبار$
$تتم مناقشة القسمة على 5 أدناه: الرقم يقبل القسمة على 5 إذا كان مكان وحداته هو 0 أو 5. ضع في اعتبارك الأرقام التالية القابلة للقسمة على 5، باستخدام اختبار القسمة على$
$تتم مناقشة القسمة على 6 أدناه: يكون الرقم قابلاً للقسمة على 6 إذا كان قابلاً للقسمة على 2 و 3 معًا. خذ بعين الاعتبار الأعداد التالية التي تقبل القسمة على 6، باستخدام اختبار قابلية القسمة على 6: 42$
$القسمة على 8 تمت مناقشتها أدناه: يكون الرقم قابلاً للقسمة على 8 إذا كانت الأرقام المكونة من الأرقام الثلاثة الأخيرة قابلة للقسمة على 8. خذ بعين الاعتبار الأرقام التالية القابلة للقسمة على 8$
$تتم مناقشة القسمة على 7 أدناه: نحتاج إلى مضاعفة الرقم الأخير من الرقم ثم طرحه من الرقم المتبقي. وإذا كانت النتيجة قابلة للقسمة على 7، فسيكون الرقم الأصلي كذلك$
$يكون الرقم قابلاً للقسمة على 9، إذا كان مجموعه من مضاعفات 9 أو إذا كان مجموع أرقامه يقبل القسمة على 9. خذ بعين الاعتبار الأرقام التالية التي تقبل القسمة على 9، باستخدام اختبار القسمة على 9:$
$القسمة على 10 تمت مناقشتها أدناه. يكون الرقم قابلاً للقسمة على 10 إذا كان يحتوي على صفر (0) في مكان وحدته. خذ بعين الاعتبار الأعداد التالية التي تقبل القسمة على 10 باستخدام اختبار قابلية القسمة على 10:$
$المضاعف المشترك الأصغر (LCM) لعددين أو أكثر هو أصغر رقم يمكن قسمته تمامًا على كل رقم محدد. المضاعف المشترك الأصغر أو المضاعف المشترك الأصغر لعددين أو أكثر هو الأصغر بين جميع المضاعفات المشتركة.$
$ما هي المضاعفات؟$
$ما هي الأعداد الأولية والمركبة؟ الأعداد الأولية هي تلك الأعداد التي لها عاملين فقط 1 والرقم نفسه. الأعداد المركبة هي تلك الأعداد التي لها أكثر من عاملين.$
$ستساعدنا ورقة العمل الخاصة بقواعد القسمة على التدرب على أنواع مختلفة من الأسئلة حول اختبار قابلية القسمة على 2، 3، 4، 5، 6، 7، 8، 9، 10 و11. نحن بحاجة إلى استخدام قواعد القسمة لمعرفة ما إذا كان المعطى أم لا الرقم يقبل القسمة على 2، 3، 4، 5، 6، 7، 8، 9، 10 و11.$

ورقة عمل حول قواعد القسمة | أسئلة حول اختبار قابلية القسمة

ستساعدنا ورقة العمل الخاصة بقواعد القسمة على التدرب على أنواع مختلفة من الأسئلة في اختبار قابلية القسمة على 2، 3، 4، 5، 6، 7، 8، 9، 10 و11. نحن بحاجة إلى استخدام قواعد القسمة لمعرفة ما إذا كان المعطى أم لا الرقم يقبل القسمة على 2، 3، 4، 5، 6، 7، 8، 9، 10 و11.