القسمة على الطرح المتكرر | القسمة كالطرح المتكرر

مدونة ضوء التعليمية تقدم لكم درس “القسمة على الطرح المتكرر | القسمة كالطرح المتكرر
” نترككم مع المقال:
كيفية القسمة بالطرح المتكرر؟
سوف نتعلم كيفية إيجاد خارج القسمة والباقي بطريقة الطرح المتكرر، وقد يتم حل مسألة القسمة.
القسمة كالطرح المتكرر
بما أن الضرب عبارة عن جمع متكرر، فإن القسمة عبارة عن طرح متكرر.
دعونا نرى كيف.
نحن نعلم أن القسمة هي التوزيع المتساوي للأشياء.
عندما نقسم، نكتشف عدد المرات التي يمكننا فيها طرح العدد المعطى من مجموعة العناصر.
دعونا نفهم هذا بمساعدة الأمثلة التالية.
1. يجب وضع 12 قلمًا بشكل متساوٍ في حاملتي الأقلام.
إذًا، كم مرة يمكن حذف 2 من 12؟
دعونا نطرح 2 مرارًا وتكرارًا من 12 حتى نصل إلى 0.
12 – 2 = 10 |  |
10 – 2 = 8 |  |
8 – 2 = 6 |  |
6 – 2 = 4 |  |
4 – 2 = 2 |  |
2 – 2 = 0 |  |
كم مرة تم طرح 2 من 12 للوصول إلى 0؟ واضح، 6
وبالتالي، 12 ÷ 2=6
أمثلة محلولة على القسمة على الطرح المتكرر:
1. حل 16 ÷ 8
حل:
يتم طرح 8 بشكل متكرر من 16 كما هو موضح:
عندما نطرح 8 من 16 مرتين، نحصل على الباقي صفر.
ومن ثم، 16 ÷ 8 = 2، 2 هو خارج القسمة.
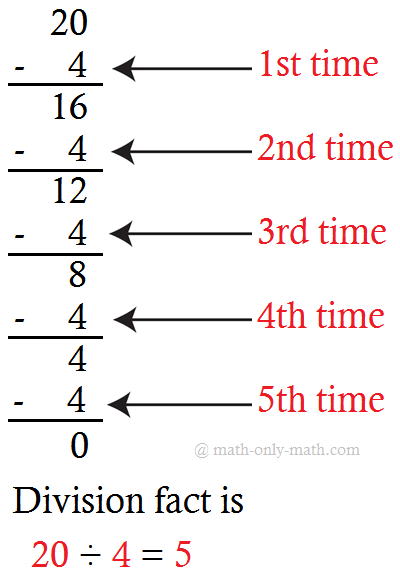
2. اقسم 20 ÷ 5
يتم طرح 5 بشكل متكرر من 20 كما هو موضح:
عندما نطرح 5 من 20 أربع مرات، نحصل على الباقي صفر.
ومن ثم، 20 ÷ 5 = 4، 4 هو خارج القسمة.
3. حل 12 في 3
حل:
يتم طرح 3 بشكل متكرر من 12 كما هو موضح:
عندما نطرح 3 من 12 أربع مرات، نحصل على الباقي صفر.
ومن ثم، 12 ÷ 3 = 4، 4 هو خارج القسمة.
4. قسّم 28 ÷ 7
يتم طرح 7 بشكل متكرر من 28 كما هو موضح:
عندما نطرح 7 من 28 أربع مرات، نحصل على الباقي صفر.
ومن ثم، 28 ÷ 7 = 4، 4 هو خارج القسمة.
5. قسّم 32 ÷ 4
يتم طرح 4 بشكل متكرر من 32 كما هو موضح:
عندما نطرح 4 من 32 ثماني مرات، نحصل على الباقي صفرًا.
وبالتالي، 32 ÷ 4 = 8، 8 هو خارج القسمة.
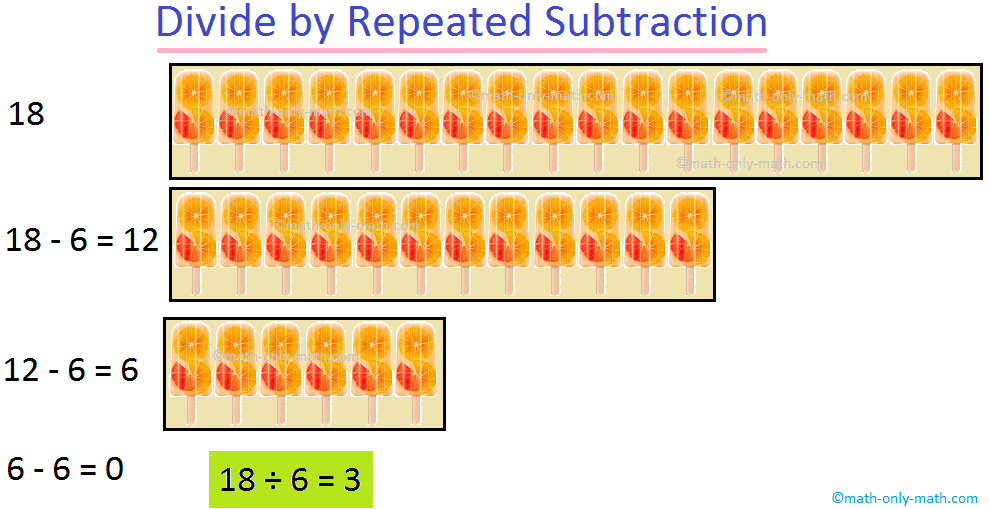
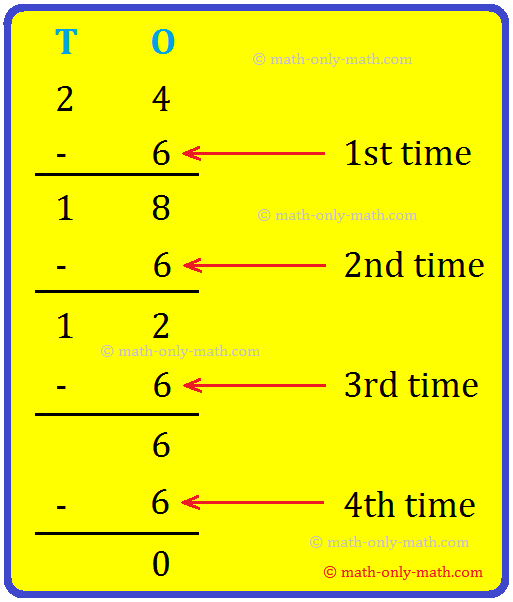
6. حل 18 في 6.
يتم طرح 6 بشكل متكرر من 18 كما هو موضح:
عندما نطرح 6 من 18 ثلاث مرات، نحصل على الباقي صفر.
ومن ثم، 18 ÷ 6 = 3، 3 هو خارج القسمة.
7. قسمي 12 زهرة في 3 مزهريات.
نضع زهرة واحدة في كل من المزهريات الثلاثة ونطرح 3 من 12 في كل مرة.
12 – 3 = 9
9 – 3 = 6
6 – 3 = 3
3 – 3 = 0
لم يعد هناك المزيد من الزهور. لقد طرحنا 4 ضرب 3 من 12.
نطرح 3 زهور 4 مرات من 12 لنحصل على 0.
7. قسم 18 آيس كريم على 6 أطفال عن طريق الطرح المتكرر.
8. ابحث عن 12 ÷ 4 بالطرح المتكرر.
مثال:
12 – 4 = 8 → 8 – 4 = 4 → 4 – 4 = 0
يمكن طرح 4 3 مرات من 12. إذن، 12 ÷ 4 = 3
القسمة كالطرح المتكرر
9. هذه سلة. هناك 15 تفاحة في السلة.

الخطوة الأولى: خذ 3 تفاحات من السلة.
تبقى 12 تفاحة في السلة.
15 – 3 = 12
الخطوة الثانية: خذ 3 تفاحات أخرى من السلة.
الآن، تبقى 9 تفاحات في السلة.
12 – 3 = 9
الخطوة الثالثة: خذ 3 تفاحات أخرى من السلة.
الآن، تبقى 6 تفاحات في السلة.
9 – 3 = 6
الخطوة الرابعة: خذ 3 تفاحات أخرى من السلة.
الآن، تبقى 3 تفاحات في السلة.
6 – 3 = 3
الخطوة الخامسة: الآن، خذ 3 تفاحات أخرى من السلة.
نجد أنه لم يبق أي تفاحة في السلة.
3 – 3 = 0
لقد طرحنا 3 من 15 بشكل متكرر وقمنا بذلك 5 مرات.
إذن، 15 ÷ 3 = 5
وهكذا يسمى القسمة الطرح المتكرر من نفس العدد.
10. Nitheeya لديها 24 حلوى. عليها توزيعها على أصدقائها الستة. كم عدد قطع الحلوى التي ستقدمها لكل صديق؟
تبدأ بإعطاء قطعة حلوى واحدة لكل صديق وتكرر هذا الفعل حتى تنتهي جميع الحلوى. هذا يستمر 4 مرات.
يحصل كل صديق على 4 حلويات.
إذن، 24 ÷ 6 = 4
ستساعدنا الأمثلة المذكورة أعلاه في حل مسائل القسمة المختلفة لعدد مكون من رقمين على عدد مكون من رقم واحد باستخدام طريقة الطرح المتكرر.
القسمة على التوزيع المتساوي:
عندما يتم توزيع 8 كرات بالتساوي على ولدين، نكتب 8 ÷ 2 = 4

أسئلة وأجوبة حول القسمة على الطرح المتكرر:
1. القسمة باستخدام الطرح المتكرر. وقد تم القيام به بالنسبة لك.
(ط) قسمة 16 على 4.
ل 1 6 – 4 1 2 | ل 1 2 – 4 8 | ل 8 – 4 4 | ل 4 – 4 0 | 16 ÷ 4 = 4 |
(2) قسمة 6 على 2.
ل 6 – 2
| ل
| ل
| ل
| 6 ÷ 2 = __ |
(ثالثًا) قسمة 12 على 3.
ل 1 2 – 3
| ل
| ل
| ل
| 12 ÷ 3 = __ |
(رابعا) قسمة 20 على 5.
ل 2 0 – 5
| ل
| ل
| ل
| 20 ÷ 5 = __ |
(ت) قسمة 14 على 7.
ل 1 4 – 7
| ل
| ل
| ل
| 14 ÷ 7 = __ |
إجابة:
1. (ثانيا)
ل 6 – 2 4 | ل 4 – 2 2 | ل 2 – 2 0 | 6 ÷ 2 = 3 |
(ثانيا)
ل 1 2 – 3 9 | ل 9 – 3 6 | ل 6 – 3 3 | ل 3 – 3 0 | 12 ÷ 3 = 4 |
(ثالثا)
ل 2 0 – 5 1 5 | ل 1 5 – 5 1 0 | ل 1 0 – 5 5 | ل 5 – 5 0 | 20 ÷ 5 = 4 |
(رابعا)
ل 1 4 – 7 7 | ل 7 – 7 0 | 14 ÷ 7 = 2 |
2. اكتب عمليات الطرح التالية كحقائق قسمة. وقد تم القيام به بالنسبة لك.
(أنا)
(ثانيا) | 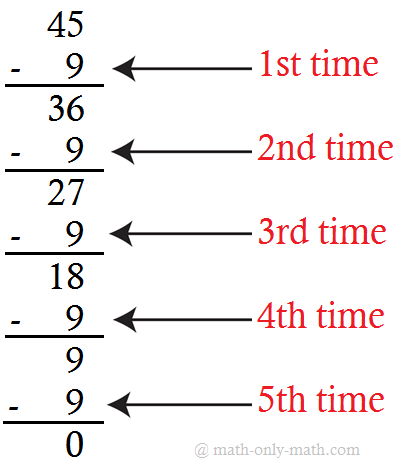 حقيقة القسمة هي _____ ÷ _____ = _____ | (ثالثا) | 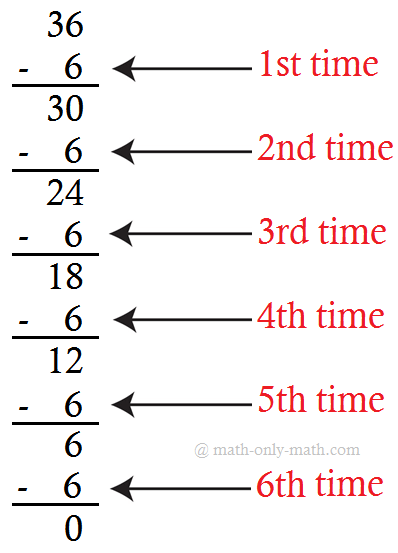 حقيقة القسمة هي _____ ÷ _____ = _____ |
إجابة:
1. (ثانيا) 45 ÷ 9 = 5
(ثالثًا) 36 ÷ 6 = 6
3. اكتب حقائق القسمة التالية في صورة عمليات طرح متكررة. وقد تم القيام به بالنسبة لك.
(ط) 20 ÷ 5 = 4
الطرح المتكرر للحقيقة المعطاة هو:
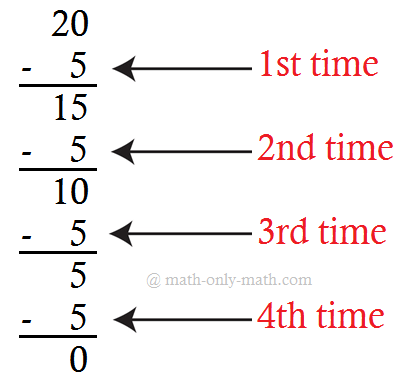
(ثانيا) | 35 ÷ 7 = 5 الطرح المتكرر للحقيقة المعطاة هو: | (ثالثا) | 48 ÷ 6 = 8 الطرح المتكرر للحقيقة المعطاة هو: |
4. اقسم ما يلي باستخدام الطرح المتكرر. لقد تم إنجاز واحد من أجلك:
(أنا) | 6 ÷ 2 6 – 2 = 4 4 – 2 = 2 2 – 2 = 0 وبالتالي، 6 ÷ 2 = 3 | (ثانيا) | 24 ÷ 8 __ ÷ __ = __ __ ÷ __ = __ __ ÷ __ = __ وبالتالي، __ ÷ __ = __ |
(ثالثا) | 18 ÷ 6 __ ÷ __ = __ __ ÷ __ = __ __ ÷ __ = __ وبالتالي، __ ÷ __ = __ | (رابعا) | 16 ÷ 4 __ ÷ __ = __ __ ÷ __ = __ __ ÷ __ = __ __ ÷ __ = __ وبالتالي، __ ÷ __ = __ |
إجابة:
4. (٢) ٢٤ ÷ ٨
24 – 8 = 16
16 – 8 = 8
8 – 8 = 0
لذلك،
24 ÷ 8 = 3
(ثانيا) 18 ÷ 6
18 – 6 = 12
12 – 6 = 6
6 – 6 = 0
لذلك،
18 ÷ 6 = 3
(ثانيا) 16 ÷ 4
16 – 4 = 12
12 – 4 = 8
8 – 4 = 4
4 – 4 = 0
لذلك،
16 ÷ 4 = 4
5. اكتب حقيقة القسمة لما يلي:
(ط) 35 – 7 – 7 – 7 – 7 – 7 → = ___ ÷ ___ = ___
(2) 20 – 5 – 5 – 5 – 5 → = ___ ÷ ___ = ___
إجابة:
5. (ط) 35 ÷ 7 = 5
(ثانيا) 20 ÷ 5 = 4
تدريبات الرياضيات للصف الثاني
من القسمة على الطرح المتكرر إلى الصفحة الرئيسية
لم تجد ما كنت تبحث عنه؟ أو تريد معرفة المزيد من المعلومات عنها الرياضيات فقط الرياضيات.
استخدم بحث Google هذا للعثور على ما تحتاجه.
اشترك في النشرة البريدية ليصلك كل جديد.





