تمثيل الكسر | البسط/المقام

تمت مناقشة تمثيل الكسر هنا. في الكسر البسيط يوجد خط أفقي. فوق هذا السطر نكتب رقما يسمى البسط.

تحت هذا السطر نكتب رقمًا آخر يسمى القاسم.

كما، \(\frac{5}{7}\) → \(\frac{\textrm{البسط}}{\textrm{المقام}}\)

في الكسر هناك رقمان. يتم كتابة رقم واحد فوق الخط الأفقي (أي 5) والآخر مكتوب تحته (أي 7). الجزء العلوي يسمى البسط والجزء السفلي يسمى المقام. يسمى الخط الأفقي بين كلا الرقمين بشريط الكسر.

في الواقع، لا يمكن التعبير عن الكسر إلا عندما نعرف حقيقتين.

(ط) إجمالي عدد الأجزاء المتساوية التي ينقسم إليها الكل. هذا هو القاسم.

(2) العدد الإجمالي للأجزاء المتساوية من الكل قيد النظر. هذا هو البسط.

على سبيل المثال، \(\frac{4}{7}\) يعني أن الكل مقسم إلى 7 أجزاء متساوية. يعتبر 4 أجزاء من نفسه. هنا، 4 هو البسط و7 هو المقام.

\(\frac{2}{5}\) كسر. 2 هو البسط و 5 هو المقام. تسمى الأرقام مثل ½، 1/3، 2/3، ¼، ¾ بالأرقام الكسرية.

مرة أخرى، \(\frac{5}{6}\) كسر، نقوله على هيئة خمسة على ستة.

وبالمثل، 7/8، 4/12. 15/10، 326/429، وما إلى ذلك، هي كسور.

الكسر يعني جزء من الرقم.

ملحوظة:

يتكون العدد الكسري من الكل وجزءه أو أجزائه.

كتابة وقراءة الكسور:

نكتب الكسور بالنظر إلى عدد الأجزاء المتساوية وعدد الأجزاء التي نشير إليها:

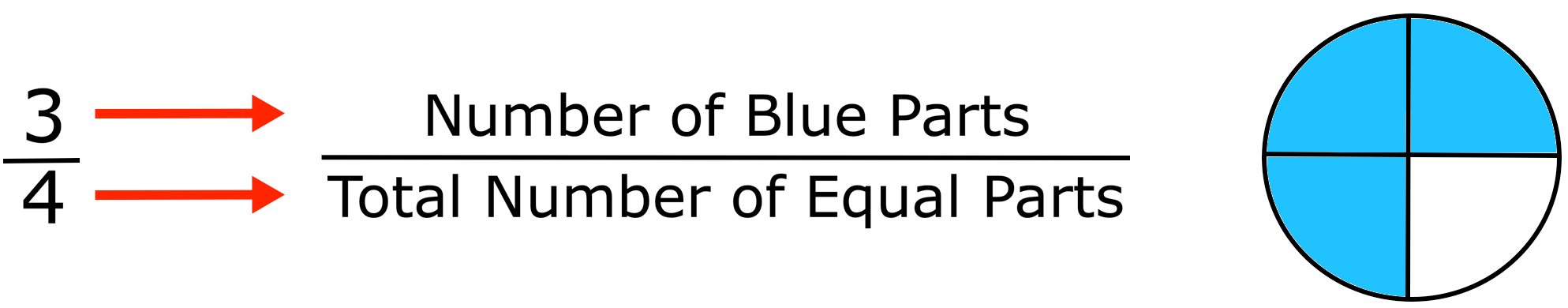
وتقرأ على أنها ثلاثة أرباع.

أسئلة وأجوبة حول تمثيل الكسر:

1. اكتب الكسور المعطاة بالكلمات. يتم واحد بالنسبة لك.

(i) \(\frac{2}{5}\) : خمسان

(2) \(\frac{1}{3}\) : __________

(ثالثًا) \(\frac{3}{4}\) : __________

(رابعا) \(\frac{5}{12}\) : __________

(ت) \(\frac{3}{8}\) : __________

الإجابات:

(الثاني) الثلث

(ثالثا) ثلاثة أرباع

(رابعا) خمسة اثني عشر

(ت) ثلاثة ثمانية

2. أعط رقم الكسر لأسماء الكسر المعطاة. يتم واحد بالنسبة لك.

(i) أربعة أتساع : \(\frac{4}{9}\)

(2) الثمن : __________

(ثالثًا) الأرباع : __________

(رابعا) الستة على ثلاثة عشر : __________

(ت) خمسة على الحادي عشر : __________

الإجابات:

(ثانيًا) \(\frac{1}{8}\)

(ثالثًا) \(\frac{1}{4}\)

(رابعا) \(\frac{6}{13}\)

(ت) \(\frac{5}{12}\)

3. اكتب الكسر للمعطى. وقد تم القيام به بالنسبة لك.

(ط) البسط = 7؛ المقام = 9 → الكسر = \(\frac{7}{9}\)

(2) المقام = 8؛ البسط = 3 → الكسر = __________

(ثالثا) البسط = 10؛ المقام = 11 → الكسر = __________

(رابعا) البسط = 8؛ المقام = 15 → الكسر = __________

(ت) المقام = 15؛ البسط = 11 → الكسر = __________

الإجابات:

(ثانيا) \(\frac{3}{8}\)

(ثالثًا) \(\frac{10}{11}\)

(رابعا) \(\frac{8}{158}\)

(ت) \(\frac{11}{15}\)

4. تحديد البسط والمقام في الكسور المعطاة.

(ط) \(\frac{1}{6}\) → البسط = ______؛ المقام = ______

(2) \(\frac{3}{7}\) → البسط = ______؛ المقام = ______

(ثالثًا) \(\frac{12}{17}\) → البسط = ______؛ المقام = ______

(رابعا) \(\frac{9}{13}\) → البسط = ______؛ المقام = ______

الإجابات:

(ط) البسط = 1؛ المقام = 6

(2) البسط = 3؛ المقام = 7

(ثالثا) البسط = 12؛ المقام = 17

(رابعا) البسط = 9؛ المقام = 13

المفهوم ذو الصلة

● جزء من الأعداد الصحيحة

● تمثيل الكسر

● الكسور المتكافئة

● خصائص الكسور المتكافئة

● مثل وخلافا للكسور

● مقارنة الكسور المتشابهة

● مقارنة الكسور التي لها نفس البسط

● أنواع الكسور

● تغيير الكسور

● تحويل الكسور إلى كسور لها نفس المقام

● تحويل الكسر إلى أصغر وأبسط صورة له

● جمع الكسور التي لها نفس المقام

● طرح الكسور التي لها نفس المقام

● جمع وطرح الكسور على خط أرقام الكسر

أنشطة الرياضيات للصف الرابع

من تمثيل الكسر إلى الصفحة الرئيسية