حقائق الضرب الأساسية | الجمع المتكرر |عملية الضرب

هناك حاجة إلى بعض حقائق الضرب الأساسية التي يجب اتباعها لضرب الأعداد. والإضافة المتكررة لنفس العدد يتم التعبير عنها بالضرب باختصار.

انظر إلى النمط التالي. هناك 5 بصمات اليد. يد واحدة هي مجموعة من خمسة أصابع.

كم عدد المجموعات المكونة من 5 أصابع؟

يمكننا أن نقول أن هناك 5 مجموعات من 5 أصابع.

دعونا نأخذ المزيد من الأمثلة على المجموعات المتساوية.

(أنا)

(ثانيا)

(ثالثا)

(4) هناك 5 مجموعات تحتوي كل منها على كرتين.

يمكن معرفة العدد الإجمالي للكرات المكونة من 5 مجموعات بكتابة 2 في 5 مجموعات أو بإضافة 2 خمس مرات بالشكل 2 + 2 + 2 + 2 + 2 = 10

يمكن أيضًا إيجاد هذا الرقم 10 بضرب 2 × 5. وبالتالي، 2 + 2 + 2 + 2 + 2 = 10 = 2 × 5 = 10

ومن ثم، فإن الجمع المتكرر لـ 2 خمس مرات يساوي 2 مضروبًا في 5.

(ت) وبالمثل، ست مجموعات مكونة من ثلاث كرات = 3 + 3 + 3 + 3 + 3 + 3 = 18

حقيقة الجمع 3 + 3 + 3 + 3 + 3 + 3 = 18 هي نفسها الضرب 3 × 6 = 18

وبالتالي، 3 × 6 = 18، أي 3 مضروبًا في 6 يساوي 18، أو 3 في 6 يساوي 18، أو حاصل ضرب 3 و6 يساوي 18.

3 × 6 = 18 تسمى حقيقة الضرب.

هذه العملية 3 × 6 = 18 هي عملية الضرب.

الرمز أو العلامة “×” هي علامة الضرب.

بنفس الطريقة:

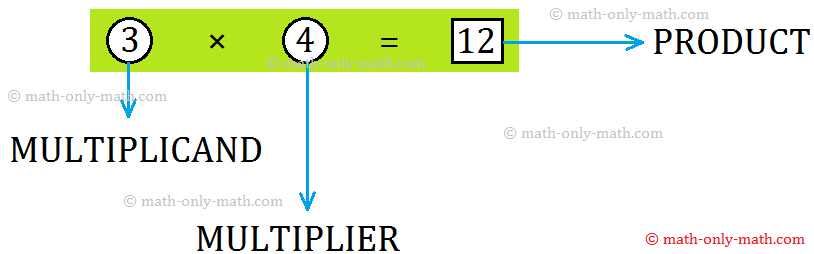
(ط) 4 + 4 + 4 = 12 هي حقيقة الجمع

(2) 4 × 3 = 12 هي حقيقة الضرب

(3) حقيقة الجمع لنفس الأعداد = حقيقة الضرب.

(4) 4 مضروبًا في 3 يساوي 12 أو 4 في 3 = 12 أو حاصل ضرب 4 و3 = 12

(5) الرمز “×” علامة الضرب.

● دعونا نلقي نظرة على الأمثلة التالية لمعرفة معنى الضرب.

على سبيل المثال:

1. إذا كانت المجموعة تحتوي على 6 موزات ويوجد مجموعتان منها، فكم عدد الموز الموجود إجمالاً؟

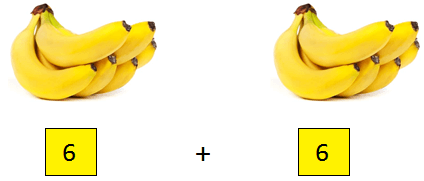
يمكن كتابة هذا على النحو التالي: 6 + 6 = 12.

تُعرف إضافة نفس الرقم مرارًا وتكرارًا بالجمع المتكرر. إذن، يوجد 12 موزة في المجمل.

باستخدام الضرب،

نكتب: 2 × 6 = 12

نقرأ: اثنان في ستة يساوي اثني عشر.

الجمع المتكرر يسمى الضرب. نستخدم الضرب فقط عندما يكون لكل مجموعة نفس العدد.

الإضافة المتكررة:

هناك 5 مجموعات، كل مجموعة تحتوي على حبتين من المانجو.

كم عدد المانجو هناك في كل شيء؟

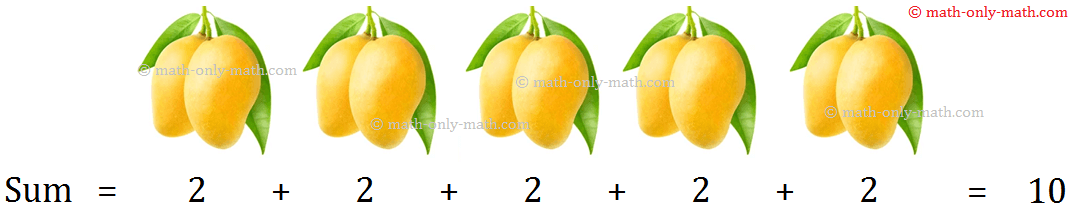
هناك ما مجموعه 10 المانجو.

نرى أن 2 يضاف 5 مرات.

يمكن كتابة ذلك بالشكل 5 ضرب 2 = 5 × 2 = 10

يتم استدعاء الإضافة المتكررة لنفس الرقم الضرب.

‘ב هو رمز الضرب ويُقرأ كـ ‘مرات‘ أو ‘مضروبة في‘.

الضرب هو وسيلة أسرع للعثور على المجموع من الجمع المتكرر.

دعونا نأخذ مثالا آخر.

هناك 4 مجموعات، كل منها 7 أوراق. كم عدد الأوراق هناك في كل شيء؟

أو يمكننا أن نقول 4 ضرب 7 = 4 × 7 = 28

2. هناك فريقان للكرة الطائرة. كل فريق لديه 3 لاعبين. كم عدد اللاعبين هناك في المجموع؟

باستخدام الجمع المتكرر،

باستخدام الضرب،

نكتب: 2 × 3 = 6

نقرأ: اثنان في خمسة يساوي عشرة.

لذلك، هناك 6 لاعبين في المجموع.

الآن، إذا كان هناك 4 فرق للكرة الطائرة. كل فريق لديه 3 لاعبين. كم عدد اللاعبين هناك في المجموع؟

باستخدام الإضافة المتكررة:

باستخدام الضرب،

نكتب: 4 × 3 = 12

نقرأ: أربعة في ثلاثة يساوي اثني عشر

لذلك، هناك 12 لاعبا في المجموع.

3. مجموعة بها 3 طيور البطريق. هناك 3 مجموعات من هذا القبيل. كم عدد طيور البطريق هناك في المجموع؟

3 + 3 + 3 = 9

نكتب: 3 × 3 = 9

نقرأ: ثلاثة في ثلاثة يساوي تسعة

لذلك، هناك 9 طيور البطريق في المجموع.

علامة الضرب:

الضرب يعني إضافة متكررة لنفس الرقم.

في الصور التالية يوجد 6 أوعية. يحتوي كل وعاء على 3 زهور.

دعونا نجد العدد الإجمالي للزهور.

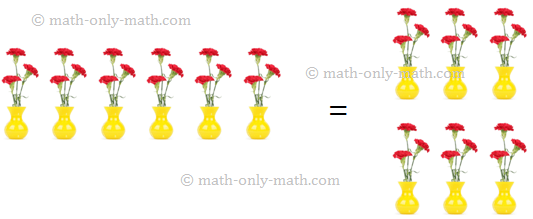
يمكننا القيام بذلك عن طريق إضافة عدد الزهور في كل وعاء.

إذن 3 + 3 + 3 + 3 + 3 + 3 = 18

هناك 6 مجموعات من 3 زهور.

إذن، لدينا ١٨ زهرة إجمالاً.

يتذكر: ‘בهو رمز الضرب.

يمكننا أيضًا كتابتها بالشكل 6 × 3 = 18.

نقرأ حقيقة الضرب على النحو التالي:

“ستة مضروبة في ثلاثة يساوي ثمانية عشر.”

الضرب هو ببساطة الجمع المتكرر لنفس العدد.

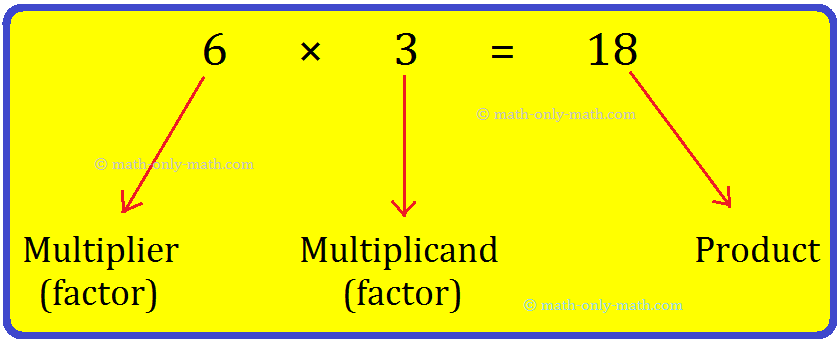
هنا،

6 يسمى المضاعف الذي يحكي كم مرة تحدث المجموعة.

3 يسمى الضرب الذي يوضح عدد العناصر في كل مجموعة.

18 يسمى منتج الذي يعطي العدد الإجمالي للكائنات.

المصطلحات المستخدمة في الضرب:

دعونا نتعلم المصطلحات المستخدمة في الضرب.

ورقة عمل حول حقائق الضرب الأساسية:

1. قم بعد وكتابة عدد المجموعات والأشياء في كل مجموعة.

(أنا)
	_____ مجموعات من _____ التفاح.
(ثانيا)
	_____ مجموعات من _____ الخفافيش.
(ثالثا)
	_____ مجموعات _____ جزر.

إجابة:

1. (ط) 4 مجموعات من تفاحتين.

(2) 3 مجموعات من 3 خفافيش

(ثالثا) 5 مجموعات من 4 جزر.

2. املأ المربعات. وقد تم القيام به بالنسبة لك.

إجابة:

2. (ثانيا) 12؛ 12

(ثالثا) 5؛ 5

3. اكتب حقيقة الضرب كما هو موضح.

(ط) 8 + 8 + 8 + 8 + 8 + 8 = __6 × 8___

(ب) 10 + 10 + 10 + 10 = __________

(ثالثًا) 11 + 11 + 11 + 11 + 11 = __________

(رابعا) 9 + 9 + 9 + 9 = __________

(ت) 7 + 7 + 7 + 7 + 7 + 7 + 7 = __________

(السادس) 4 مرات 6 = __4 × 6___

(السابع) 5 مرات 8 = __________

(ثامنا) 2 مرات 7 = __________

(التاسع) 3 ضرب 9 = __________

(خ) 4 ضرب 3 = __________

إجابة:

3. (ثانيا) 4 × 10

(ثالثا) 5 × 11

(رابعا) 4 × 9

(ت) 7 × 7

(السابع) 5 × 8

(ثامنا) 2 × 7

(التاسع) 3 × 9

(خ) 4 × 3

4. انظر إلى الرسوم التوضيحية وافهمها واملأ الفراغات.

(أنا)		___ مرات ___ = ___ البطيخ
(ثانيا)		___ مرات ___ = ___ الكرات
(ثالثا)		___ مرات ___ = ___ أقلام الرصاص

إجابة:

4. (أنا) 4 ضرب 1 = 4 بطيخات

(2) 7 ضرب 4 = 28 كرة

(ثالثًا) 4 ضرب 10 = 40 قلم رصاص

5. اكتب كإضافة متكررة.

(ط) 4 × 5 = __ + __ + __ + __

(ثانيا) 7 × 8 = __ + __ + __ + __ + __ + __ + __

(ثالثًا) 6 × 3 = __ + __ + __ + __ + __ + __

(رابعا) 10 × 1 = __ + __ + __ + __ + __ + __ + __ + __ + __

إجابة:

5. (ط) 4 × 5 = 5 + 5 + 5 + 5

(ثانيا) 7 × 8 = 8 + 8 + 8 + 8 + 8 + 8 + 8

(ثالثًا) 6 × 3 = 3 + 3 + 3 + 3 + 3 + 3

(رابعا) 10 × 1 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

6. انظر إلى حقيقة الضرب واكتب الحدود كما هو موضح.

إجابة:

6. (ثانيا) 7؛ 8؛ 56

(ثالثا) 9؛ 10؛ 90

تدريبات الرياضيات للصف الثاني

من حقائق الضرب الأساسية إلى الصفحة الرئيسية