مدونة ضوء التعليمية تقدم لكم درس “حقائق عن القسم | حقائق القسمة الأساسية
” نترككم مع المقال:
لقد تعلمنا بالفعل القسمة عن طريق الطرح المتكرر والمشاركة/التوزيع المتساوي وطريقة القسمة القصيرة. والآن، سنقرأ بعض الحقائق عن القسمة لتعلم القسمة المطولة.
I: قسمة العدد على 0:
1. إذا كان المقسوم “صفرًا” فإن أي رقم كمقسوم عليه سيعطي حاصل القسمة “صفرًا”.
مثال: إذا تم توزيع حلويات “صفر” على 8 أطفال، فمن الطبيعي أن لا يحصل أحد على أي حلويات.
ثانياً: قسمة العدد على 1:
2. إذا كان المقسوم عليه “1”، فإن أي أرباح سيكون حاصلها مساويًا لنفسه.
كم عدد أعواد الثقاب في المجموعة؟
ومن الواضح أن هناك 10 أعواد المباراة في المجموعة.
يمكننا كتابة ذلك بالصورة ١٠ ÷ 1 = 10.
عندما نقسم رقم على 1، فإن حاصل القسمة هو الرقم نفسه.
على سبيل المثال، 4 ÷ 1 = 4
15 ÷ 1 = 15
50 ÷ 1 = 50
مثال: هناك 15 قطعة حلوى؛ كل طفل يحصل على 1 حلوة. كم عدد الأطفال الذين يحصلون على الحلوى؟
ثالثاً: قسمة العدد على نفسه:
3. عندما نقسم 0 على عدد، يكون الناتج دائمًا 0.
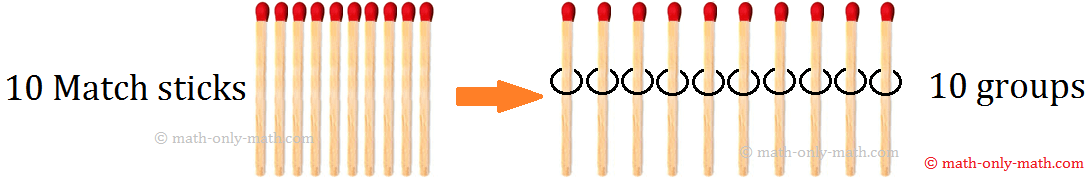
كم عدد أعواد المباراة في كل مجموعة؟
يمكننا أن نرى أن هناك 1 عصا المباراة في كل مجموعة.
يمكننا أن نكتب هذا كما
10 ÷ 10 = 1
عندما نقسم عدد على نفسه يكون حاصل القسمة دائما 1.
على سبيل المثال، 4 ÷ 4 = 1
15 ÷ 15 = 1
50 ÷ 50 = 1
رابعاً: قسمة 0 على عدد:
4. عندما نقسم 0 على عدد، يكون الناتج دائمًا 0.
على سبيل المثال، 0 ÷ 4 = 0
0 ÷ 15 = 0
0 ÷ 50 = 0
5. إن حاصل ضرب المقسوم عليه والحاصل المضاف إلى الباقي يساوي دائمًا المقسوم.
(القاسم × القسمة) + الباقي = الأرباح.
(د × ف) + ص = د
ملحوظة:
ابحث دائمًا عن المنتج أولاً ثم أضف الباقي. (وهذا يساعدنا على التحقق مما إذا كانت عملية القسمة صحيحة أم لا.)
مثال: اقسم 23 على 7
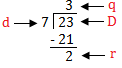
التحقق:
(د × ف) + ص = د
(7 × 3) + 2 = 23
21 + 2 = 23
23 = 23
إذن فالتقسيم صحيح.
6. في مجموع القسمة يكون الباقي دائمًا أصغر من المقسوم عليه.
مثال:
وفي المثال الأخير بوضوح يمكننا أن نرى أن الباقي (2) أقل من المقسوم عليه (7).
7. تحتوي كل حقيقة مقسومة على حقيقتين ضرب للتحقق منها.
مثال:
في القسمة 12 ÷ 6 = 2، هناك حقيقتان للضرب هما 2 × 6 = 12 و6 × 2 = 12.
8. دائمًا ما يكون حاصل القسمة والمقسوم عليه من عوامل المقسوم، إذا لم يكن هناك باقي.
مثال:
9. يكون المقسوم دائمًا مضاعفًا للقسمة والمقسوم عليه، إذا لم يكن هناك باقي.
مثال:
| د 30 5 6 | ÷ × × | د 5 6 5 | = = = | س 6 30 30 |
دعونا نراجع سريعًا ما تعلمناه عن القسمة. يتم تقسيم القسمة إلى أجزاء أو مجموعات متساوية. إنها نتيجة “التقاسم العادل”.
إذا أراد 5 أصدقاء مشاركة 15 قطعة شوكولاتة. كم عدد الشوكولاتة التي سيحصل عليها كل منهم؟ دعونا نقسم الشوكولاتة بينهم بالتساوي.
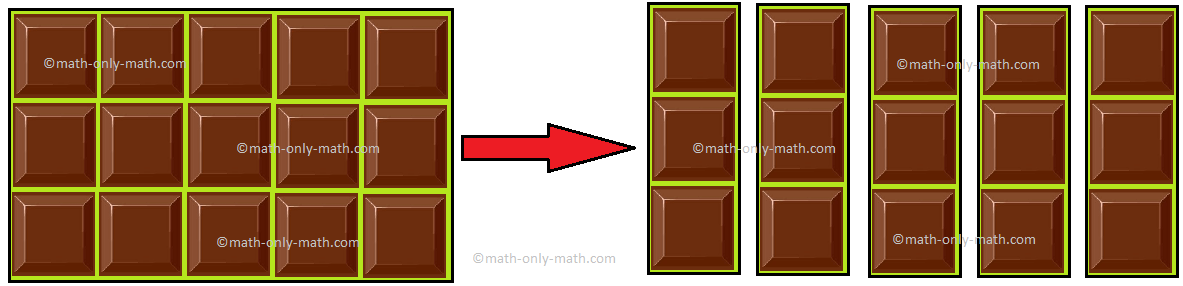
15 مقسومًا على 5 يساوي 3. يحصل كل منهما على 3.
ورقة عمل عن حقائق القسمة:
1. املأ الأرقام المفقودة:
(ط) 5 ÷ 1 = _____
(ثانيًا) 0 ÷ 8 = _____
(ثالثًا) 17 ÷ _____ =1
(رابعا) _____ ÷ 1 = 9
(ت) _____ ÷ 19 = 0
(السادس) 81 ÷ _____ =1
(7) 14 ÷ _____ =14
(ثامنا) 26 ÷ 26 = _____
(التاسع) _____ ÷ 99 = 1
إجابة:
1. (ط) 5
(ثانيا) 0
(ثالثا) 17
(رابعا) 9
(ت) 0
(السادس) 81
(السابع) 1
(ثامنا) 1
(التاسع) 99
دروس الرياضيات للصف الثالث
من حقائق حول القسم إلى الصفحة الرئيسية
لم تجد ما كنت تبحث عنه؟ أو تريد معرفة المزيد من المعلومات عنها الرياضيات فقط الرياضيات.
استخدم بحث Google هذا للعثور على ما تحتاجه.
اشترك في النشرة البريدية ليصلك كل جديد.
اكتشاف المزيد من موقع ضوء التعليمي
اشترك للحصول على أحدث التدوينات المرسلة إلى بريدك الإلكتروني.