خصائص القسمة | نظرة عامة على تقسيم الممتلكات|خصائص الرياضيات

تتم مناقشة خصائص القسمة هنا:

1. القسمة على خاصية واحدة:

إذا قسمنا رقما على 1 فإن حاصل القسمة هو الرقم نفسه.

بمعنى آخر، عندما يتم قسمة أي رقم على 1، نحصل دائمًا على الرقم نفسه باعتباره حاصل القسمة.

عندما يتم قسمة أي رقم على 1، نحصل دائمًا على الرقم نفسه.

على سبيل المثال:

(ط) 7542 ÷ 1 = 7542

(ب) 372 ÷ 1 = 372

(ثالثًا) 1522 ÷ 1 = 1522

(رابعا) 1502 ÷ 1 = 1502

(ت) 34 ÷ 1 = 34

(سادسًا) 16 ÷ 1 = 16

(ت) 1084 ÷ 1 = 1084

(6) 1745 ÷ 1 = 1745

(7) 28456 ÷ 1 = 28456

(ثامنا) 34 ÷ 1 = 34

(تاسعا) 16 ÷ 1 = 16

قسمة رقم على 1 يعطي الرقم نفسه كحاصل.

مثال:

5 ÷ 1 = 5 حيث أن 5 × 1 = 5،

8 ÷ 1 = 8 كما أن 8 × 1 = 8، إلخ.

عندما يتم قسمة رقم على 1، فإنه يعطي الرقم نفسه.

يتم إعطاء 4 بالونات لطفل واحد.

2. التقسيم على نفسه الملكية:

إذا قسمنا رقما على الرقم نفسه، فإن حاصل القسمة هو 1.

بمعنى آخر، عندما يتم قسمة أي رقم على الرقم نفسه، نحصل دائمًا على 1 باعتباره حاصل القسمة.

عندما يتم قسمة أي رقم على الرقم نفسه، نحصل دائمًا على 1 كحاصل.

على سبيل المثال:

(ط) 275 ÷ 275 = 1

(ب) 105 ÷ 105 = 1

(ثالثًا) 572 ÷ 572 = 1

(رابعا) 1027 ÷ 1027 = 1

(ت) 1426 ÷ 1426 = 1

(6) 1654 ÷ 1654 = 1

(7) 18520 ÷ 18520 = 1

(ثامنا) 7 ÷ 7 = 1

(التاسع) 24 ÷ 24 = 1

عند قسمة عدد على نفسه يكون الجواب 1

• قسم 5 قطع حلوى على 5 أطفال.

• قسم 6 تفاحات على 6 أطفال.

قسمة الرقم على نفسه يعطي 1 كحاصل.

مثال:

إذا قسمنا ست زهور على ست مزهريات، فما عدد الزهور التي يمكننا وضعها في كل مزهرية؟

نضع زهرة واحدة في كل مزهرية. إذن 6 ÷ 6 = 1 لأن 6 × 1 = 6

3. قسمة أي رقم على 0 خاصية:

تقسيم الرقم على 0 لا معنى له.

بعبارة أخرى،

القسمة على 0 لا معنى لها.

على سبيل المثال:

(ط) 15 ÷ 0 = لا معنى له

(2) 35 ÷ 0 = لا معنى

(ثالثًا) 65 ÷ 0 = لا معنى

(رابعا) 29 ÷ 0 = لا معنى

(ت) 47 ÷ 0 = لا معنى

(6) 86 ÷ 0 = لا معنى

ملحوظة: المقسوم عليه لا يمكن أن يكون صفرًا أبدًا. القسمة على صفر غير ممكنة

4. قسمة 0 على أي خاصية رقم:

0 مقسومًا على رقم يعطي 0 كحاصل.

بعبارة أخرى، عندما يتم قسمة 0 على أي رقم، نحصل دائمًا على 0 كحاصل.

قسمة الصفر على عدد يعطي الصفر كحاصل.

0 ÷ 5 = 0 لأن 5 × 0 = 0

على سبيل المثال:

(ط) 0 ÷ 25 = 0

(2) 0 ÷ 100 = 0

(ثالثًا) 0 ÷ 4255 = 0

(رابعا) 0 ÷ 15246 = 0

(ت) 0 ÷ 2 = 0

(6) 0 ÷ 75 = 75

5. القسمة على 10 و100 و1000 خاصية:

على سبيل المثال:

(ط) عندما يتم قسمة رقم على 10، فإن الرقم الموجود في المكان الأول هو الباقي.

867 ÷ 10;

حاصل القسمة = 86 و الباقي =7.

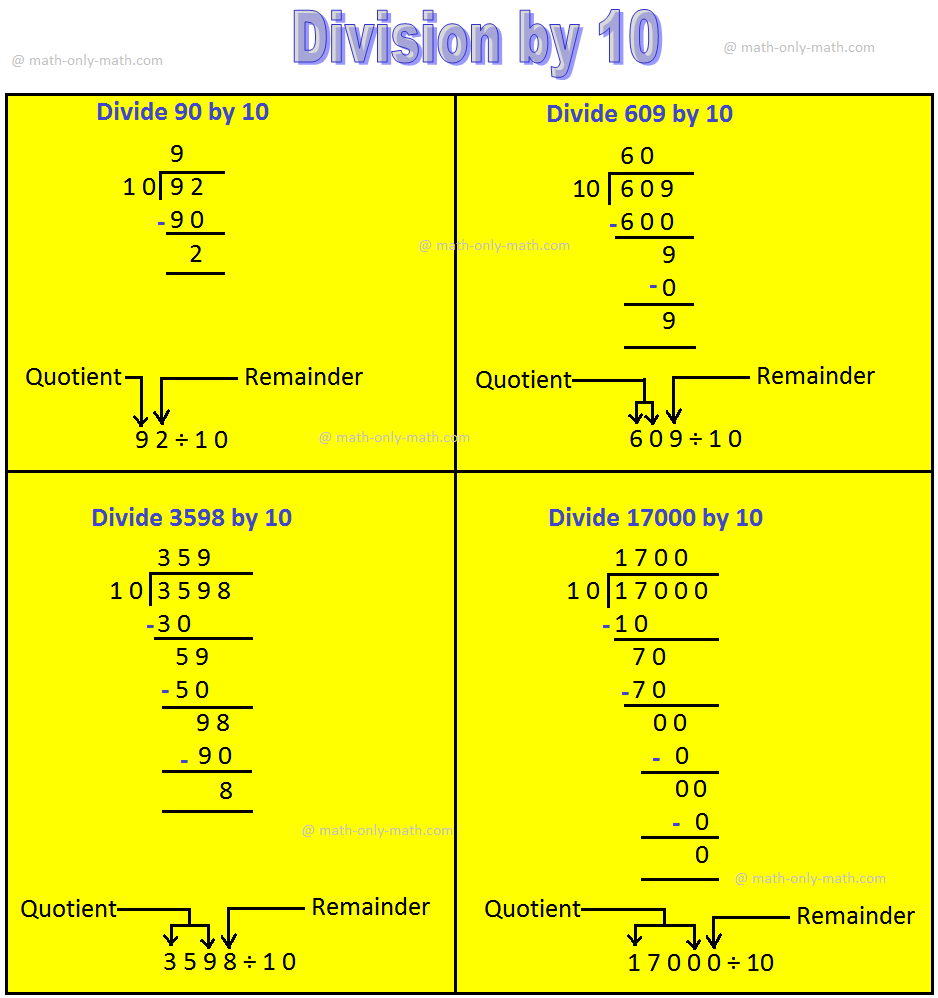
ماذا نلاحظ؟

نرى أنه عندما يتم قسمة رقم (أرباح) على 10، يتم الحصول على الناتج عن طريق إزالة رقم الآحاد من الرقم (أرباح) والرقم الموجود في خانة الآحاد هو الباقي.

(2) عند قسمة عدد على 100، فإن العدد الذي يتكون من العشرات والمكان مرة واحدة هو الباقي.

2764 ÷ 100;

حاصل القسمة = 27 و الباقي = 64.

ماذا نلاحظ؟

نحن نخيط ذلك عندما أ الرقم (الأرباح) يتم القسمة على 100 ويتم الحصول على الناتج عن طريق إزالة آخر رقمين في أقصى يمين الرقم (أرباح). الرقم الذي يتكون من هذه الأرقام الأخيرة هو الباقي.

الأسئلة المتداولة (الأسئلة الشائعة)

1. ما هو القسمة على عقار واحد؟

الإجابة: عندما يكون المقسوم عليه 1، فإن حاصل القسمة هو نفس المقسوم.

على سبيل المثال:

5 ÷ 1 = 5؛ 15 ÷ 1 = 15؛ 50 ÷ 1 = 50.

2. ما هو التقسيم في حد ذاته الملكية؟

الإجابة: عندما يكون المقسوم عليه والمقسوم هو نفس الأرقام غير الصفر، فإن حاصل القسمة هو 1.

على سبيل المثال:

7 ÷ 7 = 1؛ 13 ÷ 13 = 1؛ 70 ÷ 70 = 1.

3. ما هو قسمة 0؟

الإجابة: عندما يكون توزيع الأرباح 0، يكون حاصل القسمة 0.

على سبيل المثال:

0 ÷ 6 = 0; 0 ÷ 19 = 0; 0 ÷ 81 = 0

4. ما هي القسمة على الصفر؟

الإجابة: لا يمكن أبدًا أن يكون المقسوم عليه 0. أو أن القسمة على 0 لا معنى لها.

على سبيل المثال:

20 ÷ 0 = لا معنى له / غير محدد

52 ÷ 0 = لا معنى / غير محدد

75 ÷ 0 = لا معنى / غير محدد

ورقة عمل عن خصائص القسمة:

1. املأ الفراغات:

(ط) 6 ÷ 6 = ………..

(2) 5 ÷ 1 = ………..

(ثالثًا) 3 ÷ 3 = ………..

(رابعا) 9 ÷ 1 = ………..

(ت) 8 ÷ 8 = ………..

(6) 10 ÷ 1 = ………..

إجابة:

1. (ط) 1

(ثانيا) 5

(ثالثا) 1

(رابعا) 9

(ت) 1

(السادس) 10

2. املأ الفراغات.

(ط) 23 ÷ 23 = ………..

(2) 21 ÷ ……… = 21

(ثالثًا) 15 ÷ 1 = ………..

(رابعا) ……… ÷ 15 = 0

(ت) 0 ÷ 12 = ………

(6) 8 ÷ ……… = 1

(7) 65 ÷ 65 = ………..

(ثامنا) ……… ÷ 12 = 1

(التاسع) 8 ÷ 1 = _____

(خ) 6 ÷ 6 = _____

(الحادي عشر) 0 ÷ 10 = _____

(الثاني عشر) 21 ÷ 21 = _____

(الثالث عشر) 12 ÷ _____ = 1

(الرابع عشر) 21 ÷ 1 = _____

(الخامس عشر) _____ ÷ 12 = 0

(السادس عشر) 12 ÷ 0 = _____

إجابة:

2. (ط) 1

(ثانيا) 1

(ثالثا) 15

(رابعا) 0

(ت) 0

(السادس) 8

(السابع) 1

(ثامنا) 12

(التاسع) 8

(خ) 1

(الحادي عشر) 0

(الثاني عشر) 1

(الثالث عشر) 12

(الرابع عشر) 21

(الخامس عشر) 0

(السادس عشر) غير محدد / لا معنى له

● العمليات على الأعداد الصحيحة

● جمع الأعداد الصحيحة.

● طرح الأعداد الصحيحة.

● ضرب الأعداد الصحيحة.

● خصائص الضرب.

● قسمة الأعداد الصحيحة.

● خصائص القسمة.

مسائل الرياضيات للصف الخامس

من خصائص القسمة إلى الصفحة الرئيسية