طرح الأرقام الكاملة | عدد كامل | اطرح رقمًا كبيرًا

يمكن إجراء جمع الأرقام بأكثر من خمسة أرقام بنفس الطريقة التي تعلمنا بها القيام بطرح عدد أصغر في وقت سابق. نحن نرتب الأرقام واحدة أسفل الأخرى في الأعمدة ذات القيمة. نبدأ في طرحها واحدًا تلو الآخر من أكثر العمود والاقتراض إذا لزم الأمر ، من العمود الموجود على اليسار.

تمت مناقشة طرح الأرقام الكاملة في الخطوتين التاليتين لطرح رقم كبير من رقم كبير آخر:

الخطوة الأولى:

نحن نرتب الأرقام المعطاة في الأعمدة ، والأعداد تحت تلك ، والعشرات تحت عشرات ، والمئات من المئات وما إلى ذلك.

الخطوة الثانية:

بدءًا من تلك ، نذهب عند طرح عمود حكيمة ، والاقتراض إذا لزم الأمر ، من العمود التالي إلى اليسار.

نحن نقترض من عمود الملايين إلى مائة آلاف عمود من مائة آلاف عمود إلى عشرة آلاف عمود من عشرة آلاف عمود إلى عمود الآلاف من عمود الآلاف إلى عمود مئات من عمود مئات إلى عمود TENS ومن عمود TENS إلى عمود واحد.

على سبيل المثال:

1. طرح 2478652 من 8364579.

حل:

نقوم بترتيب الأرقام المعطاة في الأعمدة (minuend في الأعلى و subtrahend تحتها) وطرح على النحو التالي:

8364579

– 2478652

نحتاج إلى طرح العمود على العمود وعمود TENS كالمعتاد لأننا لا نحتاج هنا إلى استعارة الأرقام لأن الأرقام السفلية أصغر من الأرقام في الأعلى.

الآن نقترض مليون من 8 ملايين. ثم نحصل على (8 – 1) = 7 ملايين في العمود الملايين.

الآن بدلاً من 3 مائة آلاف ، لدينا 13 مائة آلاف في العمود مائة آلاف. الآن استعارة 1 مائة ألف من 13 مائة آلاف. ثم نحصل على (13 – 1) = 12 مائة آلاف في العمود مائة آلاف.

ثم بدلاً من 6 عشرة آلاف ، لدينا 16 عشرة آلاف في العمود العشرة الآلاف. الآن استعارة 1 عشرة آلاف من 16 عشرة آلاف. ثم نحصل على (16 – 1) = 15 عشرة آلاف في العمود العشرة آلاف.

مرة أخرى ، بدلاً من 4 آلاف ، لدينا 14 آلافًا في عمود الآلاف. الآن استعارة 1 ألف من 14 آلاف. ثم نحصل على (14 – 1) = 13 ألفًا في عمود الآلاف.

5 مئات + 1 ألف استعارة تصبح 15 مئات في العمود المئات.

لذلك ، نحن الآن بحاجة فقط إلى طرح بعد اقتراض الأرقام لأننا نلاحظ أن الأرقام السفلية أصغر من الأرقام في الأعلى.

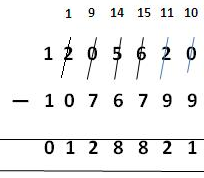
2. طرح 1076799 من 1205620.

حل:

نقوم بترتيب الأرقام المعطاة في الأعمدة (minuend في الأعلى و subtrahend تحتها) وطرح على النحو التالي:

1205620

– 1076799

في مشكلة الطرح هذه ، نلاحظ أن ما يصل إلى عشرة آلاف عمود جميع الأرقام السفلية أكبر من الأرقام في الأعلى.

لذلك ، سنبدأ في استعارة الأرقام من مائة آلاف عمود.

الآن نقترض 1 مائة ألف من مائة آلاف. ثم نحصل على (2 – 1) = 1 مائة ألف في العمود مائة آلاف.

الآن بدلاً من 0 عشرة آلاف ، لدينا 10 عشرة آلاف في العمود العشرة الآلاف. الآن استعارة 1 عشرة آلاف من 10 عشرة الآلاف. ثم نحصل على (10 – 1) = 9 عشرة آلاف في العمود العشرة آلاف.

ثم بدلاً من 5 آلاف ، لدينا 15 ألفًا في عمود الآلاف. الآن استعارة 1 ألف من 15 آلاف. ثم نحصل على (15 – 1) = 14 آلاف في عمود الآلاف.

مرة أخرى ، بدلاً من 6 مئات لدينا 16 مئات في العمود المئات. الآن استعارة 1 مائة من 16 مئات. ثم نحصل على (16 – 1) = 15 مئات في العمود المئات.

الآن بدلاً من اثنين من عشرات لدينا 12 عشرات في عمود TENS. الآن استعارة واحد عشرة من 12 عشرات. ثم نحصل على (12 – 1) = 11 TENS في عمود TENS.

0 منها + 1 عشرة استعارة تصبح 10 منها في العمود.

لذلك ، نحتاج الآن فقط إلى طرح الأرقام بعد استعارة الأرقام لأننا نلاحظ أن الأرقام السفلية أصغر من الأرقام في الأعلى.

3. طرح 3214658 من 5645789

حل:

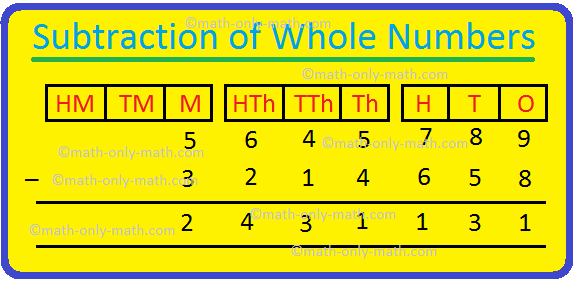
وبالتالي ، 5645789 – 3214658 = 2431131.

4. طرح 65248907 من 86165281

حل:

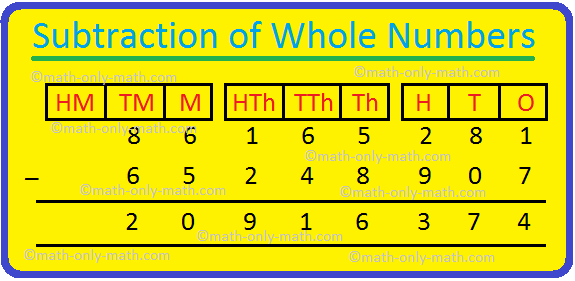
وبالتالي ، 86165281 – 65248907 = 20916374

يتم طرح أعداد أكبر أيضًا كالمعتاد. دعونا نفكر في بعض الأمثلة

5. قم بطرح 2،38،40،090 من 9،24،58،306.

حل:

توجد الأرقام المعطاة في النظام الهندي ، لذلك نضع فاصلة (،) في المبلغ وفقًا للنظام الهندي.

9 2 4 5 8 3 0 6

– 2 3 8 4 0 0 9 0

6 8 6 1 8 2 1 6

لذلك ، الجواب هو 6،86،18،216.

6. اطرح 142،098،386 من 321،836،589.

حل:

توجد الأرقام المعطاة في النظام الدولي ، لذلك نضع الفاصلة (،) في المبلغ وفقًا للنظام الدولي.

3 2 1 8 3 6 5 8 9

– 1 4 2 0 9 8 3 8 6

1 7 9 7 3 8 2 0 3

لذلك ، الجواب هو 179،738،203

مشاكل الكلمات عند طرح الأرقام الكاملة:

أنتج مصنع 313650000 حلوى في شهر ديسمبر لعيد الميلاد. من بين هذه 105224010 كانت من نكهة الخزامى. كم من الحلوى لم تكن من نكهة الخزامى؟

حل:

عدد الحلوى المنتجة = 313650000

عدد حلوى نكهة الخزامى = 105224010

عدد الحلوى التي لا تتمتع بنكهة الخزامى

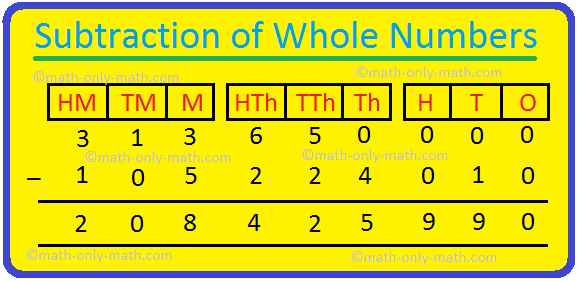
وبالتالي ، فإن إجمالي عدد الحلوى التي لا تتمتع بنكهة الخزامى = 208425990.

حل مشاكل الكلمة المعطاة عند طرح الأرقام الكاملة:

1. يبلغ عدد سكان البلد 651399888. إذا كانت 304628040 هي الإناث ، فكم ما هو ذكور؟

إجابة: 346771848

2. 1432884 زار الناس معرض الكتب الدولي يومي السبت والأحد. كان عدد الأشخاص الذين يزورون المعرض في أيام الأسبوع 89745 أقل من ذلك في عطلة نهاية الأسبوع. كم عدد الأشخاص الذين زاروا المعرض في أيام الأسبوع؟

إجابة: 1343139

3. ابحث عن الرقم الذي هو:

(ط) 30000 أقل من 183645800

(2) 1200000 أقل من 483625900

إجابة:

(ط) 183615800

(2) 482425900

ملحوظة: يمكننا طرح أرقام مكونة من 7 أرقام و 8 أرقام و 9 أرقام بنفس الطريقة التي نطرح بها أرقام مكونة من 5 أرقام و 6 أرقام.

نعلم أن الرقم الذي سيتم طرحه يُعرف باسم “subtrahend” والرقم الذي يتم طرحه منه يُعرف “minuend” والإجابة التي نحصل عليها تُعرف باسم “الاختلاف” يتم وضع الرقم أسفل الرقم منه.

● العمليات على الأرقام الكاملة

مشاكل الرياضيات في الصف الخامس

من طرح الأرقام الكاملة إلى الصفحة الرئيسية