كيفية طرح أرقام مكونة من رقمين ، مكونة من 3 أرقام ، 4 أرقام؟ | الخطوات

الطرح يعني أخذ بعض الكائنات أو الأرقام من مجموعة من الكائنات أو الأرقام. يتم استخدامه للعثور على الأرقام المتبقية. كما أنه يستخدم لمقارنة رقمين أو مجموعات.

يسمى الرقم الأكبر الذي نطرحه رقمًا أصغر منه. يسمى العدد الصغير الذي يتم طرحه من العدد الأكبر. هنا ، 5 هو Minue و 3 هو subtrahend. الجواب في الطرح يسمى الفرق. هنا ، 2 هو الفرق.

عندما نطرح رقمًا أصغر ، باستثناء: 0 ، من رقم أكبر ، يكون الفرق أصغر من Minuend.

سوف نتعلم طرح أرقام مكونة من رقمين ، والأرقام المكونة من 3 أرقام ، والأرقام المكونة من 4 أرقام ، والأرقام المكونة من 5 أرقام ، وما إلى ذلك. نحن نعلم أنه لطرح الأرقام ، نرتبها أولاً في الأعمدة القيمة ، ثم نطرح الأرقام تحت الأرقام والعشرات والمئات.

أثناء إجراء الطرح ، يتم طرح العدد الأصغر دائمًا من الرقم الأكبر. يسمى العدد الأصغر minuend ويسمى العدد الأكبر subtrahend. وتسمى النتيجة الفرق.

الآن ، حل الأسئلة التالية الواردة أدناه لتحديث المفاهيم التي تعلمناها بالفعل.

يتم استدعاء إجابة مبلغ الطرح اختلاف.

كيفية طرح أرقام من رقمين؟

تظهر الخطوات لطرح أرقام من رقمين.

طرح 39 من 78.

يصطف الأرقام وفقًا لقيمة المكان مع الحرص على وضع الرقم الأكبر في الأعلى.

في العمود لدينا 8 – 9.

لا يمكننا أن نأخذ 9 من 8 لذلك نعيد تجميع المكان التالي إلى اليسار. إعادة تجميع 78 كـ 6 عشرات و 18.

الفرق = 39

في بعض الأحيان نحتاج إلى إعادة تجميع صفوف أكثر من مرة.

كيفية طرح أرقام من 3 أرقام؟

تظهر الخطوات لطرح أرقام من 3 أرقام.

طرح 189 من 638.

إعادة تجميع 38 كـ 2 TENS 18

إعادة تجميع 62 كـ 5 عشرات 12

إجابة: 449

نتبع نفس القاعدة لطرح 4 أرقام أو أرقام أكبر.

طرح أرقام من 4 أرقام دون إعادة تجميع الفيديو

https://www.youtube.com/watch؟v=h9zied7rbte

اشترك في لدينا قناة يوتيوب للحصول على أحدث مقاطع الفيديو والتحديثات والنصائح.

كيفية طرح أرقام من 4 أرقام؟

تظهر الخطوات لطرح أرقام من 4 أرقام.

1. حل: 74834 – 38915

يصطف الرقم وفقًا لقيمة المكان.

في العمود ، يكون الرقم المراد طرحه أكبر ، لذا تم إعادة تجميع صفوفك مثل 2 TENS 14.

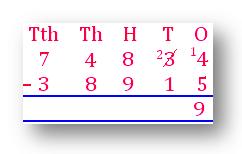
طرح عمود TENS.

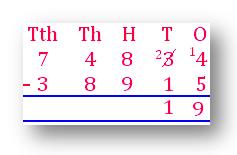
إعادة تجميع صفوف لطرح الأرقام في عمود المئات.

3 آلاف 18 مئات

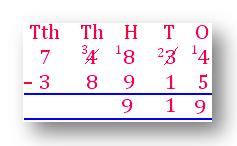
إعادة تجميع صفوف لطرح الأرقام في عمود الآلاف.

6 عشرة آلاف 13 ألف

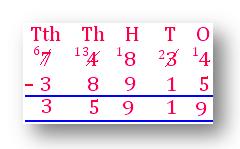
إجابة: 35919

يمكننا طرح من مكان مع الصفر. فقط تذكر إعادة تجميع المكان التالي إلى اليسار.

2. طرح: 39507 – 27386

إجابة: 12121

إعادة تجميع لطرح مكان العشرات

4 مئات 10 عشرات

كيف تتحقق من إجابة الطرح؟

طرح 2157 من 5438 وتحقق من إجابتك.

يفحص:

أضف الفرق إلى الرقم الأصغر.

سيكون الجواب هو الرقم الأصغر.

طرح الفرق من العدد الأكبر.

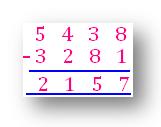
سيكون الجواب هو الرقم الأكبر.

في الطرح ، سوف نتعلم عملية الطرح للأرقام التي تحتوي على أكثر من 4 أرقام مع الاقتراض وبدون الاقتراض.

أمثلة:

1. طرح 2684 من 6795.

حل:

يتم ترتيب الأرقام في شكل العمود

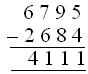
(ط) يتم طرحها ، 5 – 4 = 1

(2) يتم طرح عشرات ، 9 – 8 = 1

(3) يتم طرح المئات ، 7 – 6 = 1

(4) يتم طرح الآلاف ، 6 – 2 = 4

وبالتالي ، الفرق = 4،111

2. اطرح 6732 من 9340 (مع الاقتراض).

حل:

يتم ترتيب الأرقام في شكل العمود

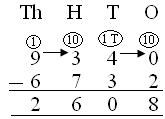
(ط) يتم طرحها ، 0 <2 ، لذلك يتم استعارة عشرة عشرة من عشرات.

الآن 1 عشرة أو 10 + 0 = 10 ، 10 – 2 = 8

(2) يتم طرح عشرات ، 3TENS – 3TENS = 0

(3) يتم طرح المئات ، و 3 مئات <7 مئات ، لذا ، يتم استعارة 1 ألف ،

لذلك 10 مئات + 3 مئات = 13 مئات ،

13 مئات – 7 مئات = 6 مئات.

(رابعا) يتم طرح الآلاف ، والآلاف 8 – 6 آلاف = 2 آلاف

وبالتالي ، الفرق = 2،608

طرح أرقام من 4 أرقام مع إعادة تجميع الفيديو

https://www.youtube.com/watch؟v=012GRBMI-VG

اشترك في لدينا قناة يوتيوب للحصول على أحدث مقاطع الفيديو والتحديثات والنصائح.

3. ما هو الفرق بين 40712 و 7549؟ (مع الاقتراض)

حل:

يتم ترتيب الأرقام في شكل العمود

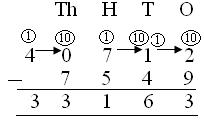
(ط) 2 <9 ، 1T أو 10 تم استعارة 10 + 2 = 12 ، 12 - 9 = 3

(II) 0 <4 ، 1H أو 10T تم استعارة 10T + 0 = 10T ، الآن 10T - 4T = 6T

(3) 6H – 5H = 1H

(4) 1 tth مستعار ، 10 – 7 = 3

(V) 3TTH – 0 = 3TTH

لذلك ، الفرق = 33،163

4. اطرح 2 3 7 4 1 2 من 6 4 9 5 2 3 (بدون استعارة)

حل:

يتم ترتيب الأرقام في شكل العمود

(ط) 3 – 2 = 1 منها

(2) 2 – 1 = 1 عشرات

(3) 5 – 4 = 1 مئات

(رابعا) 9 – 7 = 2 آلاف

(الخامس) 4 – 3 = 1 عشرة آلاف

(السادس) 6 – 2 = 4 مائة آلاف

لذلك ، الفرق = 412111

5. اطرح (مع الاقتراض) 6 5 6 2 9 من 3 2 3 4 7 8

حل:

يتم ترتيب الأرقام في شكل العمود

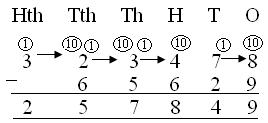
(ط) تلك: 8 <9 ، يتم استعارة 10 + 8 = 18 ، 18 - 9 = 9

(2) عشرات: 6T – 2T = 4T

(3) المئات: 4H <6H ، 1 TH أو 10H مستعار ، 10H + 4H = 14H ، 14H - 6H = 8H

(4) 2th <5 ، 1tth أو 10th مستعار 10 + 2th = 12 ، 12 - 5 = 7th

(V) 1tth <6tth ، 1thth أو 10tth مستعار 10tth + 1tth = 11tth ، 11tth - 6tth = 5tth

(السادس) بقي 2Hth كما كان.

لذلك ، الفرق = 257849

6. ابحث عن الفرق بين رقمين ، 1 4 2 7 1 3 و 3 7 4 3 9.

حل:

يتم ترتيب الأرقام في شكل العمود.

142713 أكبر من 37439 ، لذلك سيتم طرح 37439 من 142713.

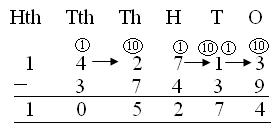
الفرق = 105274

(ط) يتم طرحها

3 <9 ، لذلك يتم استعارة 1 عشرة.

الآن 1T أو 10 + 3 = 13 ، 13 – 9 = 4

(2) يتم طرح عشرات ، 1T <3T ، لذلك يتم استعارة 1H.

الآن 1H أو 10T + 1 = 11 ،

11 – 3 = 8 ، الإجابة هي 11 – (3 + 1) = 7

(3) مائة: 6H – 4H = 2H

(4) الآلاف: 12 – 7 = 5th

(ت) عشرة آلاف: 3 – 3: = 0

(السادس) مائة ألف: 1thth – 0 = 1thth

لذلك ، 142713 – 37439 = 105274

3. العثور على الفرق.

للحصول على أمثلة:

(ط) 4 عشرة آلاف – 24 آلاف

4 عشرة آلاف → 40 الآلاف

– 24 الآلاف → – 24 ألف

16 آلاف

(2) 6 آلاف 3 مئات – 4 آلاف 17 مئات

6 آلاف 3 مئات → 5 آلاف + 13 مئات

– 4 آلاف 17 مئات → – 5 آلاف + 7 مئات

6 مئات

(3) 43 كهس – 17 كهس 23 مئات

43 كهس → 42 كهس + 100 مئات

– 17 كهس 23 مئات → – 17 كهس + 23 مئات

25 كهس + 77 مئات

أو ، 25 كهس 77 مئات

ملحوظة: يتم الطرح فقط في نفس التجميع.

ورقة العمل على الطرح:

1. تطابق الأرقام في العمودين:

إجابة:

(ط) → (ج)

(2) → (هـ)

(3) → (د)

(4) → (أ)

(ت) → (ب)

الثاني. اكتب أي رقمين يأتي قبل الأرقام المعطاة:

(ط) …………. ، …………. ، 654

(2) …………. ، …………. ، 316

(3) ……………

(رابعا) …………. ، …………. ، 999

(5) …………. ، …………. ، 100

(سادسا) …………. ، …………. ، 588

إجابة:

(ط) 652 ، 653

(2) 314 ، 315

(3) 779 ، 780

(رابعا) 997 ، 998

(5) 98 ، 99

(السادس) 586 ، 587

ثالثا. املأ الفراغات:

(ط) 346 – 100 = ………….

(2) 412 – 10 = ………….

(3) 587 – 27 = ………….

(رابعا) 697 – 590 = ………….

(ت) 962 – 15 = ………….

(سادسا) 740 – 80 = ………….

إجابة:

(ط) 246

(2) 402

(3) 560

(رابعا) 107

(5) 947

(السادس) 660

رابعا. طرح الأرقام المعطاة:

(ط) 459 – 234

(2) 762 – 430

(3) 905 – 665

(رابعا) 652 – 483

(الخامس) 790 – 548

(السادس) 809 – 719

إجابة:

(ط) 225

(2) 332

(3) 240

(رابعا) 169

(5) 242

(السادس) 90

خامسا طرح:

إجابة:

خامس (ط) 474

(2) 361

(3) 453

(رابعا) 78

(5) 147

(السادس) 525

السادس. ابحث عن الفرق بين:

(ط) 725 و 400

(2) 153 و 965

(3) 781 و 243

إجابة:

السادس. (ط) 325

(2) 812

(3) 538

السابع. ترتيب الأرقام التالية في الأعمدة وطرح:

(ط) 431 من 846

(2) 261 من 642

(3) 524 من 800

إجابة:

السابع. (ط) 415

(2) 381

(3) 276

الثامن. مشكلة الكلمة على الطرح:

(ط) ما الذي يجب إضافته إلى 243 للحصول على 605؟

(2) مجموع رقمين هو 924. إذا كان أكبر الرقمين هو 624 ، فابحث عن الرقم الأصغر.

(3) شيلي لديها سلة مليئة بالفواكه للبيع. لديها 326 ثمار معها. تبيع 180 في الصباح و 75 في المساء. كم عدد الفواكه التي لا تزال متبقية معها لبيعها؟

(رابعا) نيل ملء 437 لتر من الماء في الخزان. تستخدم عائلته 359 لترًا من الماء في يوم واحد. ما مقدار الماء الذي لا يزال في الخزان؟

الإجابات:

(ط) 362

(2) 300

(3) 71

(رابعا) 78 لتر

مفهوم ذات صلة

● إضافة

● مشاكل الكلمات في الإضافة

● الطرح

● تحقق من الطرح والإضافة

● مشاكل الكلمات التي تنطوي على الإضافة والطرح

● تقدير المبالغ والاختلافات

● ابحث عن الأرقام المفقودة

● الضرب

● اضرب رقمًا برقم من رقمين

● تكاثر رقم رقم 3 أرقام

● اضرب رقم

● تقدير المنتجات

● مشاكل الكلمات على الضرب

● الضرب والانقسام

● المصطلحات المستخدمة في التقسيم

● تقسيم من رقمين بأرقام من رقمين

● تقسيم من أربعة أرقام بأرقام من رقمين

● تقسيم بنسبة 10 و 100 و 1000

● تقسيم الأرقام

● تقدير الحاصل

● تقسيم بأرقام مكونة من رقمين

● مشاكل الكلمات في التقسيم

أنشطة الرياضيات الصف الرابع

من الطرح إلى الصفحة الرئيسية