العامل المشترك الأعلى لثلاثة أعداد باستخدام طريقة القسمة

لإيجاد العامل المشترك الأكبر لثلاثة أرقام باستخدام طريقة القسمة تمت مناقشته هنا خطوة بخطوة.

الخطوة الأولى:

أولًا، ابحث عن العامل المشترك الأكبر (HCF) لأي رقمين من الأرقام المحددة.

الخطوة الثانية:

ابحث الآن عن العامل المشترك الأعلى (HCF) للرقم الثالث المحدد والعامل المشترك الأعلى (HCF) الذي تم الحصول عليه في الخطوة 1 من الرقم الأول والثاني.

دعونا نفكر في بعض الأمثلة لإيجاد العامل المشترك الأكبر (HCF) لثلاثة أرقام بطريقة القسمة.

1. أوجد العامل المشترك الأكبر (HCF) للأعداد 184 و230 و276 باستخدام طريقة القسمة.

حل:

دعونا نوجد العامل المشترك الأكبر (HCF) للعددين 184 و230.

العامل المشترك الأعلى 184 و 230 = 46.

الآن أوجد HCF للعددين 276 و46.

العامل المشترك الأعلى 276 و 46 = 46.

ولذلك مطلوب العامل المشترك الأعلى (HCF) 184 و230 و276 = 46.

2. أوجد العامل المشترك الأكبر (HCF) للأعداد 136 و170 و255 باستخدام طريقة القسمة.

حل:

دعونا نوجد العامل المشترك الأكبر (HCF) للعددين 136 و170.

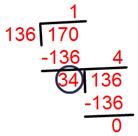
العامل المشترك الأعلى 136 و 170 = 34.

الآن أوجد HCF للعددين 34 و255.

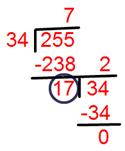
العامل المشترك الأعلى 34 و 255 = 17.

ولذلك مطلوب العامل المشترك الأعلى (HCF) 136 و170 و255 = 17.

3. باستخدام طريقة القسمة المطولة، أوجد HCF للأعداد 891 و1215 و1377.

حل:

وبالتالي، فإن العامل المشترك الأكبر للرقمين 891 و1215 هو 81 والآن سنجد HCF بقيمة 81 و1377.

وبالتالي، فإن HCF للأرقام 891 و1215 و1377 هو 81.

4. أوجد HCF للأعداد 216 و468 و828 بطريقة القسمة.

حل:

الخطوة 1: سنجد أولاً HCF بقيمة 216 و828

الخطوة 2: الآن أوجد HCF بقيمة 36 و468.

وبالتالي، HCF من 216، 468 و 828 هو 36.

5. أوجد أكبر عدد يمكن من خلاله قسمة 371 و618 و865 مع ترك الباقي 2 و3 و4 على التوالي.

حل:

عندما يتم قسمة 371 على الرقم، يتبقى 2.

وبالتالي فإن 371 – 2 = 369 يقبل القسمة على هذا الرقم.

وبالمثل، عندما يتم قسمة 618 على الرقم، يتبقى 3.

وبالتالي فإن 618 – 3 = 615 يقبل القسمة على هذا الرقم.

عندما يتم قسمة 865 على هذا الرقم، يتبقى 4.

وبالتالي فإن 865 – 4 = 861 يقبل القسمة على هذا الرقم.

وبالتالي فإن الرقم المطلوب هو HCF 369 و615 و861.

HCF 369 و615 هو 123.

HCF 123 و861 هو 123.

وبالتالي فإن العدد المطلوب هو 123.

● عوامل.

● العوامل المشتركة.

● العامل الرئيسي.

● العوامل الأولية المتكررة

● العامل المشترك الأعلى (HCF).

● أمثلة على العامل المشترك الأعلى (HCF).

● العامل المشترك الأكبر (GCF).

● أمثلة على العامل المشترك الأكبر (GCF).

● التخصيم الأولي.

● إيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي.

● أمثلة لإيجاد العامل المشترك الأعلى باستخدام طريقة التحليل الأولي.

● إيجاد العامل المشترك الأعلى باستخدام طريقة القسمة

● أمثلة لإيجاد العامل المشترك الأعلى لعددين باستخدام طريقة القسمة.

● إيجاد العامل المشترك الأعلى لثلاثة أرقام باستخدام طريقة القسمة.

صفحة أرقام الصف الخامس

مسائل الرياضيات للصف الخامس

من لإيجاد العامل المشترك الأكبر لثلاثة أرقام باستخدام طريقة القسمة إلى الصفحة الرئيسية