القسمة على خط الأعداد | مشاكل القسمة المختلفة

كيفية القسمة على خط الأعداد؟

تعلم كيفية القسمة باستخدام خط الأعداد لإيجاد خارج القسمة.

يمكننا إجراء عملية طرح متكررة على خط الأعداد لإيجاد القسمة.

1. دعونا نوجد 15 ÷ 5.

وبالتالي، 15 ÷ 5 = 3

القسمة على خط الأعداد:

لإجراء القسمة على خط الأعداد، نقوم بالعد القفزي للخلف.

2. دعونا نقسم 18 على 6 على خط الأعداد.

لتقسيم 18 على 6 على خط الأعداد، نبدأ من 18 ونقفز العد التنازلي بمقدار 6 حتى نصل إلى 0.

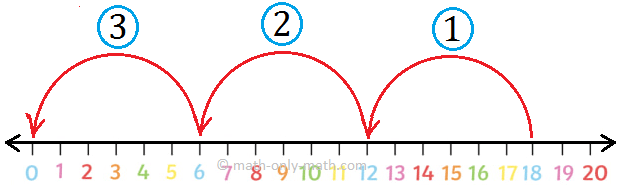
عدد القفزات هو 3.

ولذلك 18 ÷ 6 = 3.

أمثلة محلولة لإظهار القسمة على خط الأعداد:

1. حل 14 ÷ 7

حل:

يتم طرح 7 بشكل متكرر من 14 باستخدام خط الأعداد

عندما نطرح 7 مرتين من 14 على خط الأعداد، نحصل على الباقي صفر.

وبالتالي، يتم طرح 7 من 14، مرتين.

ومن ثم، 14 ÷ 7 = 2، 2 هو خارج القسمة.

2. قسّم 40 ÷ 8

باستخدام خط الأعداد، يتم طرح 8 بشكل متكرر من 40

عندما نطرح 8 5 مرات من 40 على خط الأعداد، نحصل على الباقي صفر.

وبالتالي، يتم طرح 8 من 40، 5 مرات.

ومن ثم، 40 ÷ 8 = 5، 5 هو خارج القسمة.

3. حل 24 في 6

حل:

يتم طرح 6 بشكل متكرر من 24 باستخدام خط الأعداد

عندما نطرح 6 4 مرات من 24 في خط الأعداد، نحصل على الباقي صفر.

وبالتالي، يمكن طرح 6 من 24، 4 مرات.

ومن ثم، 24 ÷ 6 = 4، 4 هو خارج القسمة.

4. اقسم 15 ÷ 3

يتم طرح 3 بشكل متكرر من 15 باستخدام خط الأعداد

يتم طرح 3 من 15، خمس مرات على خط الأعداد، ثم نحصل على الباقي صفر.

وبالتالي، يمكن طرح 3 من 15 خمس مرات.

ومن ثم، 15 ÷ 3 = 5، 5 هو خارج القسمة.

5. قسّم 63 ÷ 9

يتم طرح 9 بشكل متكرر من 63 باستخدام خط الأعداد

يتم طرح 9 من 63 سبع مرات على خط الأعداد، ثم نحصل على الباقي صفر.

وبالتالي، يمكن طرح 9 من 63 سبع مرات.

وبالتالي، 63 ÷ 9 = 7، 7 هو خارج القسمة.

على خط الأعداد، يمكننا إظهار الطرح المتكرر عن طريق العد التنازلي بقفزات متساوية.

6. اقسم 12 على 2.

ابدأ من 12. اقفز للخلف عن طريق القفز بخطوتين لكل منهما. توقف عند 0.

لاحظ أن هناك حاجة إلى 6 قفزات للوصول إلى 0.

12 – 2 = 10؛ 10 – 2 = 8؛ 8 – 2 = 6؛ 6 – 2 = 4؛ 4 – 2 = 2؛ 2 – 2 = 0

نكتب: 12 ÷ 2 = 6

نقرأ: 12 مقسومًا على 2 يساوي 6.

7. اقسم 15 على 5.

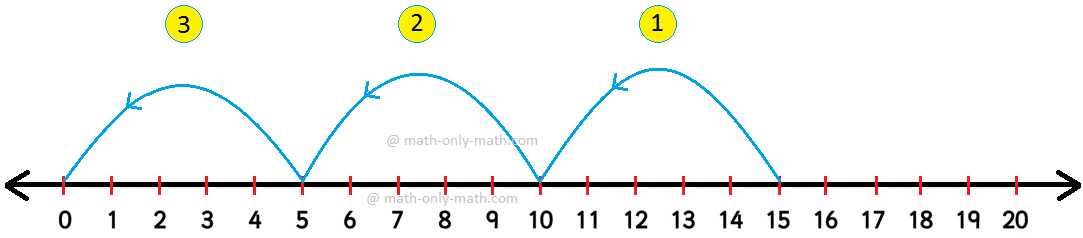
ابدأ من 15. اقفز للخلف عن طريق القيام بقفزات كل منها 5 خطوات. توقف عند 0.

لاحظ أن هناك حاجة إلى 3 قفزات للوصول إلى 0.

15 – 5 = 10؛ 10 – 5 = 5؛ 5 – 5 = 0

نكتب: 15 ÷ 5 =3

نقرأ: 15 مقسومًا على 5 يساوي 3.

القسمة على خط الأعداد

8. اقسم 12 على 4 باستخدام خط الأعداد.

يمكن استخدام خط الأعداد للقسمة. دعونا نقسم 12 على 4 باستخدام خط الأعداد.

لتقسيم 12 على 4، ضع إصبعك على الرقم 12. الآن، قم بقفزات كل منها 4 للوصول إلى 0. عدد القفزات هو 3. إذن، 12 ÷ 4 = 3.

قسمة الأعداد الصحيحة على خط الأعداد

باستخدام خط الأعداد، اكتب العدد الصحيح الذي حاصل قسمة 14 ÷ 7. بما أن القسمة تتكرر عملية الطرح، لذلك، لتقييم 14 ÷ 7، ابدأ أولًا من 14 وحرك 7 وحدات في كل مرة إلى اليسار حتى يتم الوصول إلى 0، كما هو مبين في الشكل التالي.

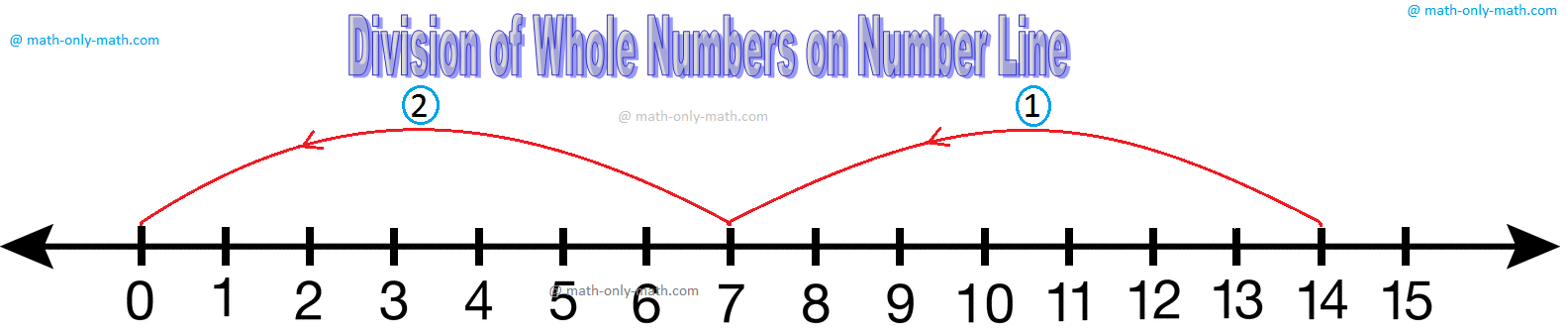
ومن ثم، 14 ÷ 7 = عدد الحركات = 2.

ستساعدنا الأمثلة المذكورة أعلاه في حل مسائل القسمة المختلفة على عدد مكون من رقم واحد وعدد مكون من رقمين على رقم واحد باستخدام خط الأعداد.

أسئلة وأجوبة حول القسمة على خط الأعداد:

1. استخدم خط الأعداد لإيجاد القسمة عن طريق الطرح المتكرر.

(ط) أوجد 12 ÷ 2

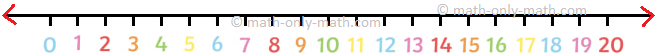
12 ÷ 2 = _____

(٢) أوجد ١٨ ÷ ٣

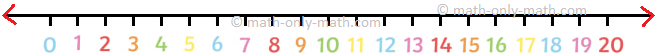
18 ÷ 3 = _____

(ثالثًا) أوجد 20 ÷ 4

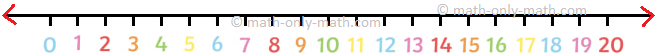
20 ÷ 4 = _____

إجابة:

(أنا) 12 ÷ 2 = 6

(ثانيا) 18 ÷ 3 = 6

(ثالثا) 20 ÷ 4 = 5

2. قسمة 6 على 3.

لذلك، 6 ÷ 3 = _____

إجابة:

2. 2

3. القسمة على خط الأعداد. وقد تم القيام به بالنسبة لك.

(أنا)

14 ÷ 2 = 7

(ثانيا)

12 ÷ 4 = _____

(ثالثا)

18 ÷ 3 = _____

(رابعا)

16 ÷ 4 = _____

(ت)

20 ÷ 4 = _____

(السادس)

10 ÷ 5 = _____

(السابع)

12 ÷ 3 = _____

إجابة:

3. (ثانيا) 3

(ثالثا) 6

(رابعا) 4

(ت) 5

(السادس) 2

(السابع) 4

4. اكتب حقيقة القسمة والطرح المتكرر لكل مما يلي. أظهر أيضًا القسمة على خط الأعداد.

(ط) 16 علبة بسكويت مقسمة بالتساوي بين 8 أطفال

حقيقة القسمة: _____ ÷ _____ = _____

الطرح المتكرر: ____________________

القسمة على خط الأعداد:

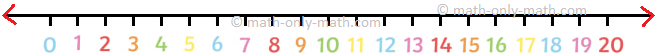
(2) 18 قطعة حلوى موزعة بالتساوي على 6 أولاد

حقيقة القسمة: _____ ÷ _____ = _____

الطرح المتكرر: ____________________

القسمة على خط الأعداد:

(رابعا) 20 لعبة موزعة بالتساوي على 4 فتيات

حقيقة القسمة: _____ ÷ _____ = _____

الطرح المتكرر: ____________________

القسمة على خط الأعداد:

إجابة:

4. (ط) حقيقة القسمة: 16 ÷ 8 = 2

الطرح المتكرر: 16 – 8 – 8 = 0

(2) حقيقة القسمة: 18 ÷ 6 = 3

الطرح المتكرر: 18 – 6 – 6 – 6 = 0

(ثالثًا) حقيقة القسمة: 20 ÷ 4 = 5

الطرح المتكرر: 20 – 4 – 4 – 4 – 4 – 4 = 0

تدريبات الرياضيات للصف الثاني

من القسمة على خط الأعداد إلى الصفحة الرئيسية