تحويل الكسور إلى العشرية | أمثلة حل

في تحويل الكسور إلى العشرية ، نعلم أن الكسور العشرية هي الكسور مع القواسم 10 ، 100 ، 1000 إلخ. من أجل تحويل الكسور الأخرى إلى العشرية ، نتبع الخطوات التالية:

الخطوة الأولى: قم بتحويل الكسر إلى جزء مكافئ مع المقام 10 أو 100 أو 1000 إذا لم يكن الأمر كذلك.

الخطوة الثانية: خذ البسط الكسر المعطى. ثم حدد النقطة العشرية بعد مكان أو مكانين أو ثلاثة أماكن من اليمين إلى اليمين إذا كان مقام الكسر المعطى هو 10 أو 100 أو 1000 على التوالي.

لاحظ أن؛ أدخل الأصفار على يسار البسط إذا كان لدى البسط أرقام أقل.

● لتحويل جزء يضم 10 في المقام ، وضعنا النقطة العشرية في مكان واحد اليسار من الرقم الأول في البسط.

على سبيل المثال:

(i) \ (\ frac {6} {10} \) = .6 أو 0.6

(II) \ (\ frac {16} {10} \) = 1.6

(iii) \ (\ frac {116} {10} \) = 11.6

(IV) \ (\ frac {1116} {10} \) = 111.6

● لتحويل جزء يمتلك 100 في المقام ، وضعنا النقطة العشرية في المكانين اليسار من الرقم الأول في البسط.

على سبيل المثال:

(i) \ (\ frac {7} {100} \) = 0.07

(II) \ (\ frac {77} {100} \) = 0.77

(iii) \ (\ frac {777} {100} \) = 7.77

(IV) \ (\ frac {7777} {100} \) = 77.77

● لتحويل جزء يحتوي على 1000 في المقام ، وضعنا النقطة العشرية ثلاثة أماكن متبقية من الرقم الأول في البسط.

على سبيل المثال:

(i) \ (\ frac {9} {1000} \) = 0.009

(II) \ (\ frac {99} {1000} \) = 0.099

(iii) \ (\ frac {999} {1000} \) = 0.999

(IV) \ (\ frac {9999} {1000} \) = 9.999

ستساعدنا المشكلة على فهم كيفية تحويل الكسر إلى عشري.

في \ (\ frac {351} {100} \) سوف نغير الكسر إلى عشري.

اكتب أولاً البسط ثم قسّم البسط على المقام وإكمال القسم.

ضع النقطة العشرية بحيث يكون عدد الأرقام في الجزء العشري هو نفس عدد الأصفار في المقام.

دعنا نتحقق من تقسيم العشرية من خلال إظهار الانقسام العشري خطوة بخطوة.

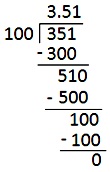
نحن نعلم أنه عندما يكون العدد الذي تم الحصول عليه عن طريق تقسيمه على المقام هو الشكل العشري للكسر.

يمكن أن يكون هناك حالتان في تحويل الكسور إلى العشرية:

• عندما يتوقف التقسيم بعد عدد معين من الخطوات حيث يصبح الباقي صفرًا.

• عندما يستمر التقسيم حيث يوجد ما تبقى بعد كل خطوة.

هنا ، سنناقش متى يكتمل القسم.

شرح على الطريقة باستخدام مثال خطوة بخطوة:

• قسّم البسط على المقام وإكمال التقسيم.

• إذا تم ترك الباقي غير الصفر ، فضع النقطة العشرية في الأرباح والحصنت.

• الآن ، ضع الصفر على يمين الأرباح وإلى يمين الباقي.

• قسّم كما في حالة عدد كامل عن طريق تكرار العملية أعلاه حتى يصبح الباقي صفرًا.

1. تحويل \ (\ frac {233} {100} \) إلى عشري.

حل:

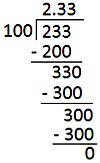
2. التعبير عن كل مما يلي كما العشرية.

(i) \ (\ frac {15} {2} \)

حل:

\ (\ frac {15} {2} \)

= \ (\ frac {15 × 5} {2 × 5} \)

= \ (\ frac {75} {10} \)

= 7.5

(جعل المقام 10 أو قوة أعلى من 10)

(II) \ (\ frac {19} {25} \)

حل:

\ (\ frac {19} {25} \)

= \ (\ frac {19 × 4} {25 × 4} \)

= \ (\ frac {76} {100} \)

= 0.76

(iii) \ (\ frac {7} {50} \)

حل:

\ (\ frac {7} {50} \) = \ (\ frac {7 × 2} {50 × 2} \) = \ (\ frac {14} {100} \) = 0.14

ملحوظة:

سيتم تحويل الكسور إلى العشرية عندما لا يمكن تحويل المقام إلى 10 أو قوة أعلى من 10 في تقسيم العشرية.

قواعد العمل لتحويل الكسور إلى العشرية:

لتحويل جزء مشترك إلى رقم عشري ، يتعين علينا اتباع الخطوات التالية.

الخطوة الأولى: قم بتغيير الكسر المشترك المعطى إلى جزء مكافئ يكون مقامه 10 أو 100 أو 1000 ، إلخ.

الخطوة الثانية: عد عدد الأصفار في المقام بعد 1.

الخطوة الثالثة: في البسط ، ابدأ من اليمين المتطرف وحرك النقطة العشرية إلى

أمثلة على تحويل الكسور إلى العشرية:

1. تحويل الكسور التالية إلى عشرية.

(i) \ (\ frac {3} {4} \)

(II) 5 \ (\ frac {1} {2} \)

(iii) \ (\ frac {31} {125} \)

حل:

(i) \ (\ frac {3} {4} \) = \ (\ frac {3 × 25} {4 × 25} \) = \ (\ frac {75} {100} \) = 0.75

(ii) 5 \ (\ frac {1} {2} \) = \ (\ frac {11} {2} \) = \ (\ frac {11 × 5} {2 × 5} \) = \ (\ frac {55} {10} \) = 5.5

(iii) \ (\ frac {31} {125} \) = \ (\ frac {31 × 8} {125 × 8} \) = \ (\ frac {248} {1000} \) = 0.248

2. تحويل 2 \ (\ frac {7} {16} \) إلى عشري.

حل:

2 \ (\ frac {7} {16} \) = \ (\ frac {2 × 16 + 7} {16} \) = \ (\ frac {32 + 7} {16} \) = \ (\ frac {39} {16} \)

الآن ، \ (\ frac {39} {16} \) = \ (\ frac {39 × 625} {16 × 625} \) = \ (\ frac {24375} {10000} \) = 2.43755

وهكذا ، \ (\ frac {39} {16} \) = 2.4375

3. التعبير عن الكسور التالية كما العشرية:

(أنا) \ (\ frac {3} {10} \)

حل:

باستخدام الطريقة أعلاه ، لدينا

\ (\ frac {3} {10} \)

= 0.3

(الثاني) \ (\ frac {1479} {1000} \)

حل:

\ (\ frac {1479} {1000} \)

= 1.479

(ثالثا) 7 \ (\ frac {1} {2} \)

حل:

7 \ (\ frac {1} {2} \)

= 7 + \ (\ frac {1} {2} \)

= 7 + \ (\ frac {5 × 1} {5 × 2} \)

= 7 + \ (\ frac {5} {10} \)

= 7 + 0.5

= 7.5

(رابعا) 9 \ (\ frac {1} {4} \)

حل:

9 \ (\ frac {1} {4} \)

= 9 + \ (\ frac {1} {4} \)

= 9 + \ (\ frac {25 × 1} {25 × 4} \)

= 9 + \ (\ frac {25} {100} \)

= 9 + 0.25

= 9.25

(الخامس) 12 \ (\ frac {1} {8} \)

حل:

12 \ (\ frac {1} {8} \)

= 12 + \ (\ frac {1} {8} \)

= 12 + \ (\ frac {125 × 1} {125 × 8} \)

= 12 + \ (\ frac {125} {1000} \)

= 12 + 0.125

= 12.125

تحويل جزء شائع إلى جزء عشري:

لتحويل جزء مشترك إلى جزء عشري ، نتبع طريقة التقسيم. في هذه الطريقة ، نتخذ هذه الخطوات.

قواعد العمل لتحويل جزء مشترك إلى جزء عشري:

الخطوة الأولى: قسّم البسط على المقام حتى يتم الحصول على الباقي غير الصفر.

الخطوة الثانية: ضع نقطة عشرية في الأرباح وكذلك في الحاصل.

الخطوة الثالثة: ضع صفرًا على يمين النقطة العشرية في الأرباح الموزعة وكذلك على يمين الباقي عند الحاجة.

الخطوة الرابعة: قسّم مرة أخرى تمامًا كما نفعل بأعداد كاملة.

الخطوة الخامسة: كرر الخطوة الرابعة حتى الباقي هو الصفر.

أمثلة على تحويل جزء شائع إلى جزء عشري:

1. تحويل إلى عشري.

(أنا) \ (\ frac {3} {4} \)

(2) 4\ (\ frac {1} {4} \)

حل:

(ط) قسّم البسط 3 على المقام 4.

لذلك ، \ (\ frac {3} {4} \) = 0.75

(II) 4 \ (\ frac {1} {4} \)

قم بتحويلها أولاً إلى جزء غير لائق

4 \ (\ frac {1} {4} \) = \ (\ frac {4 × 4 + 1} {4} \) = \ (\ frac {17} {4} \)

الآن ، قسّم البسط 17 على المقام 4.

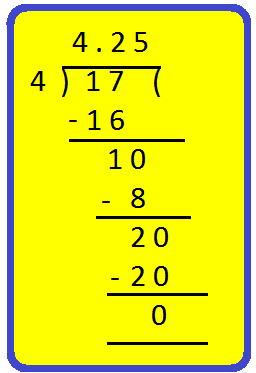
لذلك ، 4 \ (\ frac {1} {4} \) = 4.25

ورقة عمل حول تحويل الكسور إلى العشرية:

1. تحويل الأرقام الكسرية التالية إلى أرقام عشرية:

(i) \ (\ frac {7} {10} \)

(II) \ (\ frac {23} {100} \)

(iii) \ (\ frac {172} {100} \)

(IV) \ (\ frac {4905} {100} \)

(V) \ (\ frac {9} {1000} \)

(vi) \ (\ frac {84} {1000} \)

(i) \ (\ frac {672} {1000} \)

(i) \ (\ frac {4747} {1000} \)

الإجابات:

(ط) 0.7

(2) 0.23

(3) 1.72

(رابعا) 49.05

(ت) 0.009

(السادس) 0.084

(ط) 0.672

(ط) 4.747

2. التعبير عن الكسور التالية كأرقام عشرية:

(i) \ (\ frac {2} {5} \)

(II) \ (\ frac {9} {25} \)

(iii) \ (\ frac {8} {20} \)

(IV) \ (\ frac {22} {100} \)

(V) 2 \ (\ frac {3} {4} \)

(vi) 9 \ (\ frac {7} {25} \)

(VII) \ (\ frac {205} {125} \)

(viii) 16 \ (\ frac {16} {40} \)

(IX) \ (\ Frac {5926} {1000} \)

إجابة:

2. (ط) 0.4

(2) 0.36

(3) 0.4

(رابعا) 0.22

(5) 2.75

(السادس) 9.36

(السابع) 1.64

(الثامن) 16.4

(التاسع) 5.926

● مفهوم ذات صلة

● العشرية

● أرقام عشرية

● الكسور العشرية

● مثل العشرية

● مقارنة العشرية

● أماكن عشرية

● تحويل على عكس العشرية إلى العشريات العشرية

● توسع عشري وكسر

● إنهاء عشرية

● غير العشري غير المنهاء

● تحويل الكسور إلى الكسور

● تحويل الكسور إلى العشرية

● HCF و LCM من العشرية

● تكرار أو متكرر عشري

● نقي متكرر عشري

● مختلطة متكررة عشرية

● قاعدة بودم

● قواعد Bodmas/Pemdas – بما في ذلك العشرية

● قواعد PEMDAS – تتضمن أعداد صحيحة

● قواعد PEMDAS – تنطوي على العشرية

● قاعدة بيمداس

● قواعد Bodmas – تنطوي على أعداد صحيحة

● تحويل العشرية المتكررة النقية إلى جزء مبتذ

● تحويل العشرية المتكررة المختلطة إلى كسور مبتذلة

● تبسيط العشري

● تقريب العشرية

● التقريب العشري إلى أقرب رقم كامل

● التقريب العشري إلى أقرب أعشار

● التقريب العشري إلى أقرب مائة

● جولة عشرية

● مضيفا العشرية

● طرح العشرية

● تبسيط العشرات التي تنطوي على العشرية والطرح العشري

● مضاعفة العشرية برقم عشري

● مضاعفة العشرية بفارق عدد كامل

● تقسيم العشري على عدد كامل

● تقسيم العشري على عدد عشري

مشاكل الرياضيات في الصف السابع

من تحويل الكسور إلى العشرية إلى الصفحة الرئيسية