حقائق القسمة الأساسية | القسمة معكوس الضرب |الرياضيات
مدونة ضوء التعليمية تقدم لكم درس “حقائق القسمة الأساسية | القسمة معكوس الضرب |الرياضيات
” نترككم مع المقال:
هناك حاجة إلى بعض حقائق القسمة الأساسية التي يجب اتباعها لتقسيم الأعداد. يتم التعبير عن الطرح المتكرر لنفس العدد بالقسمة بشكل قصير وطويل.
عندما يتم توزيع كائنات المجموعة بالتساوي، فإننا نسمي ذلك القسمة. دعونا نفهم المفهوم أعلاه من خلال بعض الأمثلة:
1. شارك 12 قلم رصاص بين طفلين. للعثور على عدد أقلام الرصاص التي سيحصل عليها كل طفل، نبدأ بإعطاء قلم رصاص واحد لكل طفل حتى يتبقى لدينا أقلام رصاص.
هذا يعني أنه قد تم تقسيم 12 قلمًا إلى مجموعتين، كل منهما 6 أقلام رصاص. يحصل كل طفل على 6 أقلام رصاص.
وهذا يعني أن هناك مجموعتين من 6.
هذا مكتوب كما 12 ÷ 2 = 6
وهذا ما يسمى حقيقة القسمة.
ملحوظة: “÷” هو رمز القسمة.
في مجموع القسمة:
- العدد الذي نقسمه يسمى أرباح.
- ويسمى الرقم الذي نقسم عليه المقسوم عليه.
- تسمى نتيجة القسمة حاصل.
على المثال أعلاه 12 ÷ 2 = 6
12 هو الأرباح ،
2 هو المقسوم عليه و
6 هو الحاصل.
2. لنفترض أن لديك 18 بالونة. قسمهم بالتساوي بين 3 أطفال.
حل:
دعونا نوزع 18 بالونة بالتساوي على 3 أطفال.
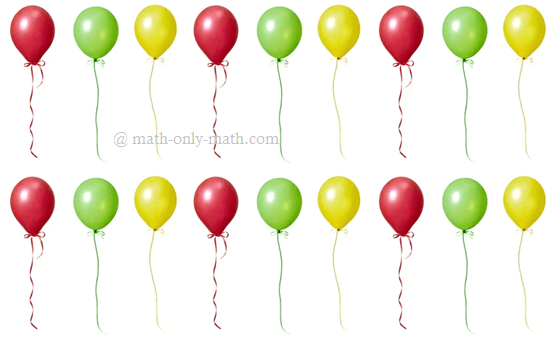
كل طفل لديه 6 بالونات.
نكتبها بالشكل 18 ÷ 3 = 6.
نحن نقول ذلك 18 مقسومًا على 3 يساوي 6.
18 ÷ 3 = 6 يسمى أ حقيقة التقسيم.
3. يجب أن يكون هناك 12 مانجو. يجب توزيع هذه المانجو بالتساوي على 4 أولاد.
دعونا نوزع 12 مانجو على الأولاد الأربعة بشكل منفصل للحصول على المانجو. أولا وقبل كل شيء يتم وضع مانجو واحدة لكل صبي.
نرى أنه قد بقي عدد من المانجو. ثم يتم وضع مانجو أخرى لكل ولد. لا يزال هناك المانجو المتبقية.
الآن يتم وضع مانجو ثالثة لكل ولد. الآن أصبح لدى كل ولد 3 حبات مانجو ولم يتبق أي مانجو في الخارج.
عند إضافة المانجو لكل ولد نحصل عليه؛

3 مانجو + 3 مانجو + 3 مانجو + 3 مانجو = 12 مانجو
يعني: 3 مانجو 4 مرات = 12
أو 3 × 4 = 12
إنه يثبت حقيقة الضرب 3 × 4 = 12. ومرة أخرى، إذا أخذنا 3 أربع مرات من 12، نحصل على صفر.
يعني 12 – 3، أربع مرات = 0، 12 ÷ 3 = 4
أو 12 ÷ 4 = 3
ومن هنا نحصل على،
(ط) 3 أربع مرات أو أربع مرات 3 يوضح حقيقة الضرب:
3 × 4 = 12
أو 4 × 3 = 12
(2) 3 أخرجت 4 مرات توضح حقيقة القسمة الأساسية:
12 ÷ 3 = 4
أو 12 ÷ 4 = 3
ومن ثم فإن التوزيع بالتساوي أو تكوين مجموعات من عدد متساو من العناصر يوضح حقيقة القسمة.
(ط) إضافة نفس الرقم بشكل متكرر يظهر حقيقة الضرب:
(3 + 3 + 3 + 3 = 4 × 3 = 12)
(2) طرح نفس العدد بشكل متكرر يوضح حقيقة القسمة:
(12 – 3 – 3 – 3 – 3 = 0؛ 12 ÷ 3 = 4)
وبالتالي فإن عملية القسمة هي عكس الضرب وعملية الضرب هي عكس القسمة.
ولذلك نعلم أيضاً أن؛
(ط) 3 × 4 = 12 يعطي حقيقتين قسمتين كما يلي: 12 ÷ 3 = 4 و 12 ÷ 4 = 3
(2) 12 ÷ 3 = 4 يعطي حقيقتين ضرب مثل 3 × 4 = 12 و4 × 3 = 12.
المزيد من الأمثلة:
4. دعونا نلقي نظرة على المثال التالي لنرى ما يعنيه القسمة.
يوجد 12 عودًا من الورود و4 أواني زهور.

ضع عددًا متساويًا من الزهور في كل إناء للزهور.
أولاً، ضع عود وردة واحداً في كل إناء للزهور.
 |  12 – 4 = 8 |
ثم ضع عود وردة آخر في كل إناء للزهور.
 |  8 – 4 = 4 |
استمر حتى لا يتبقى أي عصي ورد.
 |  4 – 4 = 0 |
نجد أن كل وعاء زهور يحتوي على 3 أعواد ورد.
يمكن كتابة هذا على النحو التالي: 12 – 4 = 8؛ 8 – 4 = 4؛ 4 – 4 = 0
يُعرف طرح نفس العدد مرارًا وتكرارًا باسم متكرر
الطرح.
باستخدام القسمة
نكتب: 12 ÷ 4 =3
نقرأ: 12 مقسومًا على 4 يساوي 3.
الطرح المتكرر يسمى القسمة. نحن نستخدم القسمة فقط عندما نريد المشاركة بالتساوي.
المشاركة المتساوية
1. بريا لديها قطعة من الشوكولاتة مكونة من 6 قطع. إنها تريد ذلك
شاركها بالتساوي مع صديقتها راهول. كم قطعة من
الشوكولاته سوف يحصل كل واحد منهم؟
أعط قطعة واحدة لكل منهم.
إعطاء واحد أكثر لكل منهما.
استمر حتى لا توجد قطع متبقية.
نجد أن كل صديق يحصل على 3 قطع من الشوكولاتة.
يمكن كتابة هذا على النحو التالي:
6 – 2 = 4؛ 4 – 2 = 2؛ 2 – 2 = 0
أو، 6 ÷ 2 = 3
2. يتم إعطاؤك 4 أقلام رصاص.
شارك بالتساوي مع صديقك.
4 – 2 = 2
2 – 2 = 0
أو، 4 ÷ 2 = 2
3. سيتم توزيع 8 تفاحات بالتساوي على 4 أطفال. كم عدد التفاحات التي سيحصل عليها كل طفل؟
دعونا نعطي تفاحة واحدة لكل طفل. سيتم ترك 4 تفاحات في السلة.
دعونا نعطي تفاحة واحدة إضافية لكل طفل. لم يبق أي تفاحة في السلة.
نلاحظ أنه عند تقسيم 8 تفاحات بالتساوي بين 4 أطفال، يحصل كل طفل على تفاحتين.
المشاركة المتساوية هي قسم.
8 ÷ 4 = 2
رمز القسمة هو “÷“، ويُقرأ على أنه “مقسم على”.
التجمع المتساوي
يجب تقسيم 20 تفاحة إلى حصص متساوية وحفظها في السلال. إذا وضعنا 5 تفاحات في سلة واحدة، فكم عدد السلات المطلوبة؟

ضع 5 تفاحات في سلة واحدة.

ضع 5 تفاحات أخرى في سلة أخرى.
 |  |
ضع 5 تفاحات أخرى في سلة أخرى.
لا يزال هناك تفاحات متبقية، لذا ضع 5 تفاحات أخرى في سلة أخرى.
الآن لم يعد هناك المزيد من التفاح.
لذلك، هناك حاجة إلى 4 سلال في المجموع.
يمكن كتابة هذا على النحو التالي: 20 – 5 = 15؛ 15 – 5 = 10؛ 10 – 5 = 5؛ 5 – 5 = 0
أو، 20 ÷ 5 = 4
تحديد الأرباح والمقسوم عليه والحاصل في بيان القسمة المحدد.

دعونا نتذكر بعض الحقائق المهمة حول القسمة.
- القسمة تعني الانقسام إلى مجموعات متساوية.
- القسمة هي الطرح المتكرر.
- القسمة عكس الضرب.
في قسمة مجموع العدد المراد تقسيمه يسمى أرباح. العدد الذي نقسم عليه يسمى المقسوم عليه. نتيجة القسمة تسمى حاصل.
مراجعة الشعبة :
• عندما نشكل مجموعات متساوية، نستخدم القسمة.
• علامة القسمة هي ÷
• العدد المقسوم على نفسه يساوي 1
على سبيل المثال 7 ÷ 7 = 1 أو 4 ÷ 4 = 1 أو 9 ÷ 9 = 1
• الرقم المقسوم على 1 يساوي الرقم نفسه.
على سبيل المثال 2 ÷ 1 = 2 أو 5 ÷ 1 = 5 أو 8 ÷ 1 = 8
• صفر مقسوم على أي عدد يساوي صفر.
على سبيل المثال 0 ÷ 3 = 0 أو 0 ÷ 6 = 0 أو 0 ÷ 10 = 0
أسئلة وأجوبة حول حقائق القسمة الأساسية:
I. اكتب حقائق القسمة باستخدام رمز القسمة لكل صورة.
(ط) مشاركة 8 محايات بين طفلين.
 | 8 ÷ 2 = 4 |
(2) مشاركة 4 مقصات بين طفلين.
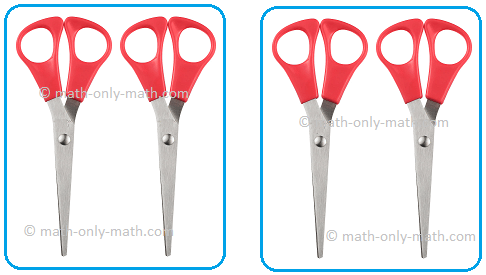 | 4 ÷ __ = __ |
(3) مشاركة 14 مفتاحًا بين طفلين.
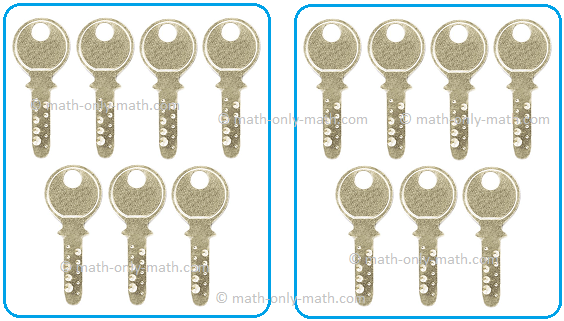 | 14 ÷ __ = __ |
(4) مشاركة 12 قلمًا بين طفلين.
 | 12 ÷ __ = __ |
إجابة:
أنا. (2) 4 ÷ 2 = 2
(ثالثًا) 14 ÷ 2 = 7
(رابعا) 12 ÷ 2 = 6
ثانيا. املأ الفراغات –
(ط) 0 ÷ 5 = _____
(ب) 0 ÷ 6 = _____
(ثالثًا) 0 ÷ 8 = _____
(رابعا) 0 ÷ 9 = _____
(ت) 4 ÷ 1 = _____
(السادس) 3 ÷ 1 = _____
(السابع) 2 ÷ 1 = _____
(ثامنا) 6 ÷ 1 = _____
(التاسع) 2 ÷ 2 = _____
(خ) 5 ÷ 5 = _____
(الحادي عشر) 6 ÷ 6 = _____
(الثاني عشر) 8 ÷ 8 = _____
(13) 7 ÷ 1 = _____
(الرابع عشر) 3 ÷ 3 = _____
(الخامس عشر) 0 ÷ 2 = _____
(السادس عشر) 6 ÷ 1 = _____
(السابع عشر) 8 ÷ 1 = _____
(الثامن عشر) 9 ÷ 1 = _____
(التاسع عشر) 0 ÷ 4 = _____
(xx) 5 ÷ 1 = _____
(الحادي والعشرون) 0 ÷ 3 = _____
(الثاني والعشرون) 0 ÷ 7 = _____
(الثالث والعشرون) 9 ÷ 9 = _____
(الرابع والعشرون) 1 ÷ 1 = _____
إجابة:
ثانيا. (ط) 0
(ثانيا) 0
(ثالثا) 0
(رابعا) 0
(ت) 4
(السادس) 3
(السابع) 2
(ثامنا) 6
(التاسع) 1
(خ) 1
(الحادي عشر) 1
(الثاني عشر) 1
(الثالث عشر) 7
(الرابع عشر)1
(الخامس عشر) 0
(السادس عشر) 6
(السابع عشر) 8
(الثامن عشر) 9
(التاسع عشر) 0
(xx) 5
(الحادي والعشرون) 0
(الثاني والعشرون) 0
(الثالث والعشرون) 1
(الرابع والعشرون) 1
ثالثا. املأ الفراغات –
(ط) 6 ÷ _____ = 6
(ثانيا) 2 ÷ _____ = 2
(ثالثًا) 2 ÷ _____ = 1
(رابعا) 4 ÷ _____ = 0
(ت) _____ ÷ 9 = 0
(السادس) _____ ÷ 8 = 1
(السابع) _____ ÷ 3 = 3
(ثامنا) _____ ÷ 2 = 1
(التاسع) 5 ÷ _____ = 1
(خ) 7 ÷ _____ = 1
(الحادي عشر) 6 ÷ _____ = 6
(12) 1 ÷ _____ = 3
(13) _____ ÷ 7 = 0
(رابع عشر) _____ ÷ 1 = 8
(١٥) _____ ÷ 6 = 1
(السادس عشر) 6 ÷ _____ = 0
رابعا. ضع عددًا متساويًا من الكرات في كل كيس.
وقد تم القيام به بالنسبة لك.
(ط) ضع 15 كرة في 3 أكياس.

(2) ضع 6 كرات في كيسين.
 |  |
(3) ضع 9 كرات في 3 أكياس.
(رابعا) ضع 10 كرات في 5 أكياس.
(ت) ضع ١٥ كرة في ٥ أكياس.
V. كم عدد المجموعات سيكون هناك؟
تظهر من حيث الطرح والقسمة المتكررة.
وقد تم القيام به بالنسبة لك.
(أنا) |  | يتم توزيع 10 كرات في مجموعات مكونة من 5 كرات. 10 – 5 = 5؛ 5 – 5 = 0 10 ÷ 5 = 2 لذلك، سيكون هناك مجموعتين. |
(ثانيا) |  | 6 قفازات توضع في أزواج ____________ ____________ ____________ |
(ثالثا) |  | 10 قذائف ليتم وضعها في مجموعات من ____________ ____________ ____________ |
(رابعا) |  | 12 كتابًا يتم وضعها في مجموعات ____________ ____________ ____________ |
(ت) |  | 30 قطعة حلوى يتم وضعها في مجموعات مكونة من 10 قطع. ____________ ____________ ____________ |
سادسا. املأ المربعات:
(أنا)

تم تقسيم ١٨ كتابًا بالتساوي إلى _____ مجموعات.
تحتوي كل مجموعة على _____ كتب.
حقيقة القسمة هي 18 ÷ 6 = _____
(ثانيا)

تم تقسيم 24 ثمرة مانجو بالتساوي _____ المجموعات.
تحتوي كل مجموعة _____ المانجو.
حقيقة القسمة هي 24 ÷ 6 = _____
(ثالثا)

تم تقسيم 30 موزة بالتساوي إلى مجموعات.
تحتوي كل مجموعة على _____ موز.
حقيقة القسمة هي _____ ÷ _____ = _____
(رابعا)

تم تقسيم 8 قطع حلوى بالتساوي إلى مجموعات.
تحتوي كل مجموعة على _____ حلوى.
حقيقة القسمة هي _____ ÷ _____ = _____
(ت) العد والقسمة.

يتم الاحتفاظ بـ 9 تفاحات بالتساوي في 3 سلال.
حقيقة القسمة هي _____ ÷ _____ = _____
تحتوي كل سلة على _____ تفاح.
(السادس) العد والتقسيم.
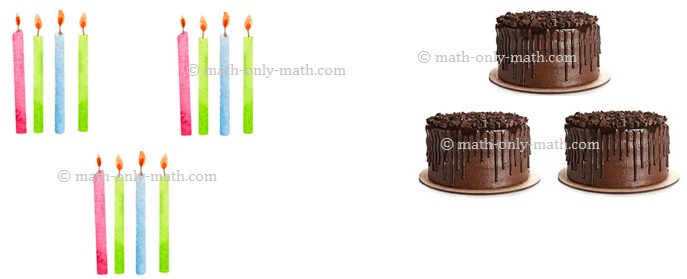
12 شمعة توضع بالتساوي على 3 قطع كيك.
حقيقة القسمة هي _____ ÷ _____ = _____
تحتوي كل كعكة على _____ شموع.
تدريبات الرياضيات للصف الثاني
من حقائق القسمة الأساسية إلى الصفحة الرئيسية
لم تجد ما كنت تبحث عنه؟ أو تريد معرفة المزيد من المعلومات عنها الرياضيات فقط الرياضيات.
استخدم بحث Google هذا للعثور على ما تحتاجه.
اشترك في النشرة البريدية ليصلك كل جديد.





