طرح الأعداد باستخدام خط الأعداد |الطرح بخط الأعداد

مدونة ضوء التعليمية تقدم لكم درس “طرح الأعداد باستخدام خط الأعداد |الطرح بخط الأعداد
” نترككم مع المقال:

سيساعدنا طرح الأعداد باستخدام خط الأعداد على معرفة كيفية استخدام خط الأعداد لطرح رقم واحد من رقم آخر.

يمكن فهم عملية طرح الأعداد جيدًا بمساعدة خط الأعداد.

ضع في اعتبارك القواعد التالية للحركات على خط الأعداد لطرح رقم معين من رقم آخر:

(ط) ضع علامة على كلا الرقمين المعطاين على نفس خط الأعداد، كل منهما يبدأ من الصفر.

(2) من الرقم الثاني (أي الرقم الذي سيتم طرحه)، أوجد عدد الخطوات اللازمة للوصول إلى موضع الرقم الأول.

هذا العدد من الخطوات هو الجواب المطلوب.

ملحوظة:

(ط) إذا كان عدد الخطوات التي تم التحرك بها نحو اليمين، فإن الإجابة هي رقم موجب.

(2) إذا كان عدد الخطوات التي تم التحرك بها باتجاه اليسار، فإن الإجابة تكون رقمًا سالبًا.

طرح الأعداد باستخدام خط الأعداد في مواقف مختلفة:

1. طرح عدد موجب من عدد موجب.

على سبيل المثال: أوجد باستخدام خط الأعداد (+6) – (+2).

قم بتمييز مواضع الأرقام +6 و +2 على نفس خط الأعداد.

الآن قم بحساب عدد الخطوات اللازمة من موضع الرقم +2 للوصول إلى موضع الرقم +6. نجد أنه على بعد 4 خطوات إلى اليمين.

وبالتالي، (+6) – (+2) = +4 أو ببساطة 4.

2. طرح عدد سالب من عدد موجب.

على سبيل المثال: قم بالتقييم باستخدام خط الأعداد (+5) – (-3).

حدد موضع الرقمين +5 و -3 على نفس خط الأعداد.

$طرح عدد سالب من عدد موجب$

الآن بدءًا من الموضع -3، احسب عدد الخطوات اللازمة للوصول إلى +5. انظر أيضا الاتجاه. نجد أنه يتعين علينا التحرك 8 خطوات إلى اليمين.

ولذلك، (+5) – (-3) = +8

3. طرح عدد موجب من عدد سالب.

على سبيل المثال: قم بالتقييم باستخدام خط الأعداد (-7) – (+2).

بعد وضع علامة على موضع -7 و+2 على نفس خط الأعداد، قم بالعد من موضع +2 عدد الخطوات والاتجاه اللازم للوصول إلى -7.

$طرح عدد موجب من عدد سالب$

نجد أن هناك 9 خطوات إلى اليسار.

وبالتالي، (-7) – (+2) = -9

4. طرح عدد سالب من عدد سالب.

على سبيل المثال: أوجد القيمة باستخدام خط الأعداد (-6) – (-4).

حدد موضع الرقمين -6 و -4 على نفس خط الأعداد.

$طرح عدد سالب من عدد سالب$

الآن قم بحساب عدد الخطوات اللازمة من موضع الرقم -4 للوصول إلى موضع الرقم -6. نجد أنه على بعد خطوتين إلى اليسار.

ولذلك، (-6) – (-4) = -2

طرح الأعداد الصحيحة على خط الأعداد

يمكن أيضًا عرض عملية طرح عددين صحيحين على خط الأعداد.

1. دعونا نجد 8 – 5.

$طرح الأعداد الصحيحة على خط الأعداد$

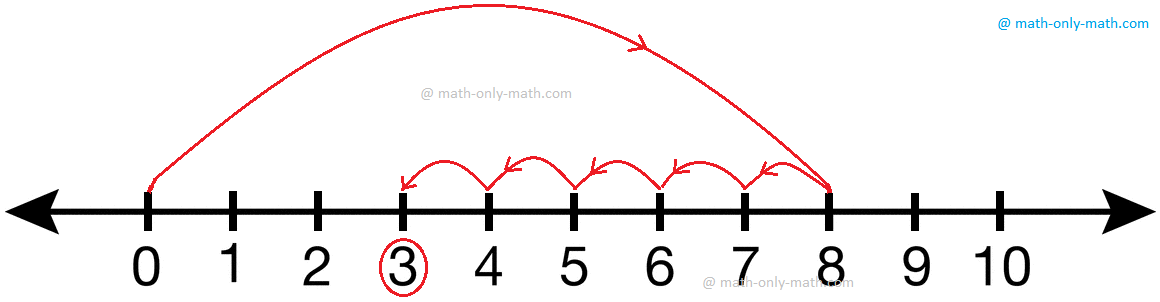
النقطة الموجودة عند طرف السهم الأطول هي 8. ابدأ من 8. بما أنه يتم طرح 5، تحرك نحو اليسار بقفزة واحدة بمقدار وحدة واحدة، وقم بإجراء 5 قفزات من هذا القبيل. نصل إلى النقطة 3. وبالتالي، 8-5-3

2. باستخدام خط الأعداد، اكتب العدد الصحيح الناتج عن طرح 4 من 9.

للعثور على 9 – 4، ابدأ من 9 واتجه 4 وحدات إلى اليسار لتحصل على 5، كما هو موضح في الشكل التالي.

$الطرح على خط الأعداد$

ومن ثم، 9 – 4 = 5

الطرح باستخدام خط الأعداد

نحن نعلم أن الطرح يعني “الأخذ”.

3. دعونا نطرح ٥ من ١٨ على خط الأعداد.

لطرح 5 من 18 على خط الأعداد، نبدأ من 18 ونعد 5 خطوات إلى الوراء.

$الطرح باستخدام خط الأعداد$

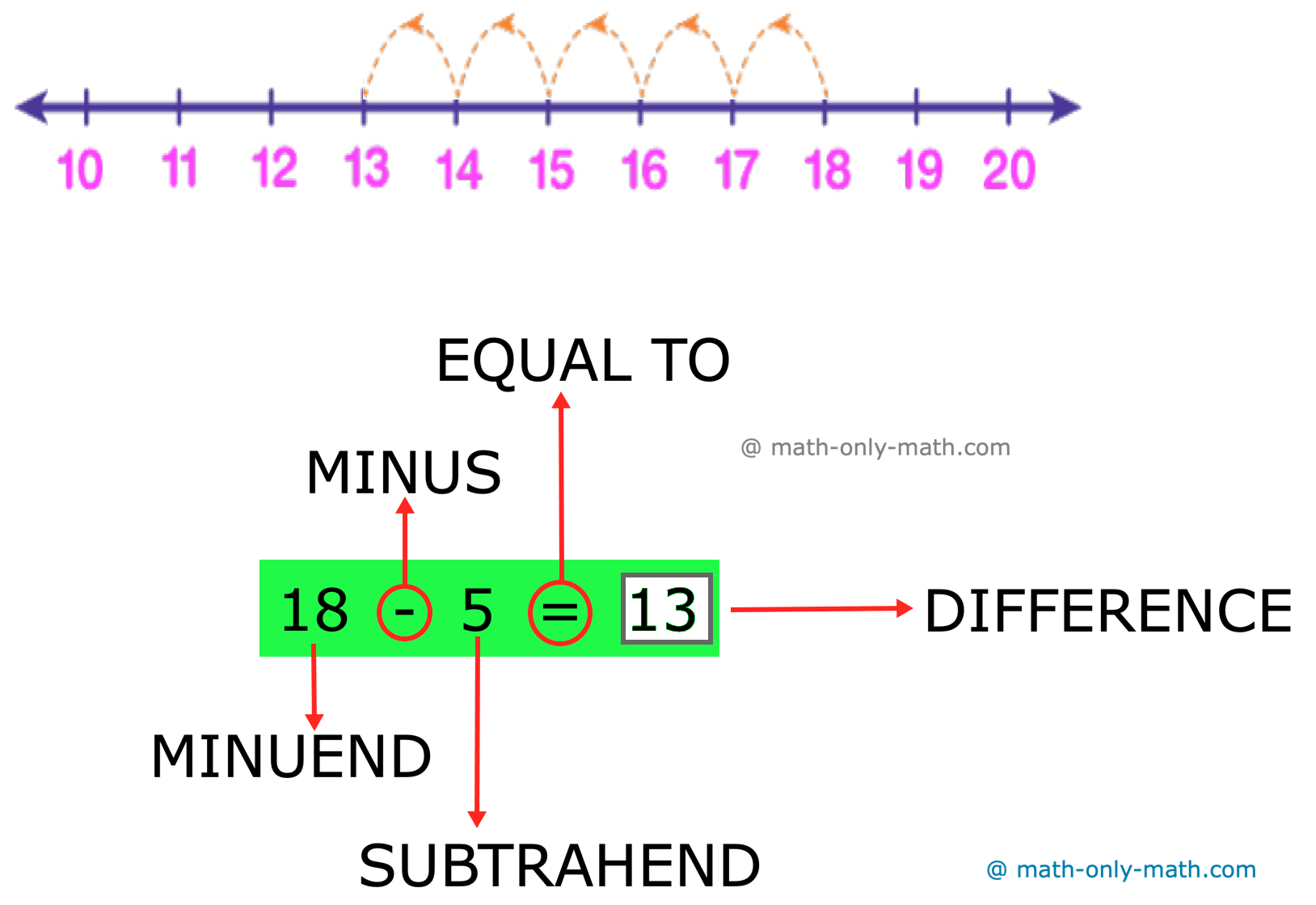
الرقم الذي يتم طرحه يسمى طرح، ويسمى الرقم الذي يتم طرحه منه تذكير والنتيجة تسمى اختلاف.

الجواب الذي نحصل عليه بعد الطرح يسمى اختلاف.

قد ترغب في هذه

$الأعداد الطبيعية هي جميع الأعداد من 1 فصاعدا، أي 1، 2، 3، 4، 5، …... وتستخدم في العد. نحن نعلم منذ الصغر أننا نستخدم الأرقام 1، 2، 3، 4، 5، 6، ………..$

عد الأعداد الطبيعية | تعريف الأعداد الطبيعية | عد

الأعداد الطبيعية هي جميع الأعداد من 1 فصاعدا، أي 1، 2، 3، 4، 5، …… وتستخدم في العد. نحن نعلم منذ الصغر أننا نستخدم الأرقام 1، 2، 3، 4، 5، 6، ………..
$عند قراءة الأعداد الكبيرة وكتابتها، نقوم بتجميع القيم المكانية في فترات$
$يتم استخدام الأرقام للحساب والعد. تسمى أرقام العد 1، 2، 3، 4، 5، .......... بالأعداد الطبيعية. لوصف عدد العناصر في المجموعة التي لا تحتوي على كائنات$
$خصائص جمع الأعداد الصحيحة هي كما يلي: خاصية الإغلاق: إذا كان a و b عددين صحيحين، فإن a + b هو أيضًا عدد صحيح. وبعبارة أخرى، مجموع أي عددين صحيحين$
$هناك ست خصائص لضرب الأعداد الصحيحة ستساعد على حل المسائل بسهولة. خصائص الضرب الستة هي خاصية الإغلاق، خاصية التبادل، خاصية الصفر، خاصية الهوية، خاصية الترابط، وخاصية التوزيع.$
$إجراءات تقدير المبلغ والفرق موجودة في الأمثلة التالية. مثال 1: قم بتقدير المجموع 5290 + 17986 عن طريق تقدير الأعداد إلى أقرب (1) مئات (2) آلاف.$
$إجراءات تقدير المنتج والحاصل موجودة في الأمثلة التالية. مثال 1: قدّر الناتج 958 × 387 عن طريق تقريب كل عامل إلى مكانه الأكبر.$
$خصائص الأعداد الصحيحة هي كما يلي: الرقم 0 هو أول وأصغر الأعداد الصحيحة. • جميع الأعداد الطبيعية بالإضافة إلى الصفر تسمى أعدادا صحيحة.$
$تسمى الأرقام الموجودة على الخط تمثيل الأعداد الصحيحة على خط الأعداد. يساعدنا خط الأعداد أيضًا على مقارنة رقمين صحيحين، أي تحديد أي من الرقمين الصحيحين المعطاين$
$1. عندما يتم طرح الصفر من الرقم، فإن الفرق هو الرقم نفسه. على سبيل المثال، 8931 – 0 = 8931، 5649 – 0 = 5649 2. عندما يتم طرح رقم من نفسه يكون الفرق صفرًا. على سبيل المثال، 5485 – 5485 = 0 3. عندما يتم طرح 1 من رقم، نحصل على قيمته$
$الأعداد الصحيحة هي أرقام العد بما في ذلك 0. لقد رأينا أن الأعداد 1، 2، 3، 4، 5، 6……. الخ هي أعداد طبيعية. هذه الأعداد الطبيعية مع الرقم صفر$
$ستساعدنا عملية جمع الأعداد باستخدام خط الأعداد على معرفة كيفية استخدام خط الأعداد لعملية الجمع. يمكن فهم عملية جمع الأرقام جيدًا بمساعدة خط الأعداد.$
$تدرب على الأسئلة الواردة في ورقة العمل حول قراءة وكتابة الأعداد الكبيرة لتجميع القيم المكانية في فترات من مائة وألف ومليون ومليار. الأسئلة مرتبطة بالكتابة$
$تدرب على الأسئلة الواردة في ورقة العمل حول التقدير. تعتمد الأسئلة على تقدير المجموع والفرق والحاصل والحاصل لأقرب العشرات والمئات والآلاف.$
$تتم مناقشة خصائص إضافة الأعداد الصحيحة هنا مع الأمثلة. 1. جمع (مجموع) أي عددين صحيحين هو دائمًا عدد صحيح. على سبيل المثال: (i) 5 + 9 = 14 ∈ Z (ii) (-5) + 9 = 4 ∈ Z$